柱
漢語漢字
柱,英文名為column,柱是建築物中垂直的主結構件,承托在它上方物件的重量。在中國建築中,橫樑直柱,柱陣列負責承托梁架結構及其他部分的重量,如屋檐,在主柱與地基間,常建有柱礎。另外,亦有其他較小的柱,不置於地基之上,而是置於梁架上,以承托上方物件的重量,再透過梁架結構,把重量傳至主柱之上。例如脊瓜柱或蜀柱,是在梁架之上承托部分屋檐的重量。中國古代的柱子多數為木造,屬於大木作範圍;間有石柱。為防水、防潮,木柱下墊以石質柱礎。
按截面形式分
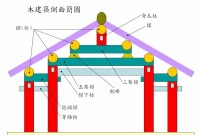
木建築側面簡圖
按所用材料分
石柱、磚柱、砌塊柱、木柱、鋼柱、鋼筋混凝土柱、勁性鋼筋混凝土柱、鋼管混凝土柱和各種組合柱;
按長細比分為

柱的其中之一
短柱在軸心荷載作用下的破壞是材料強度破壞,
長柱在同樣荷載作用下的破壞是屈曲,喪失穩定,根據歐拉公式分析。
承壓中長柱通常採用經驗公式計算。
柱是結構中極為重要的部分,柱的破壞將導致整個結構的損壞與倒坍。
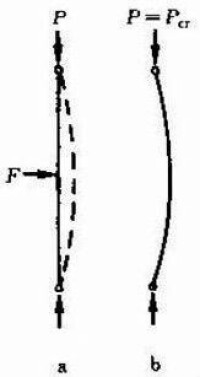
圖1 受壓柱的兩種平衡狀態
b 不能恢復原態的平衡狀態
根據細長程度的不同,柱的失效可分為:細長柱的線彈性失穩,中長柱的非線彈性失穩和短柱的強度破壞。
細長柱的線彈性失穩
細長柱失穩時應力並未超過比例極限(見材料的力學性能)。失穩后柱的受力性質起了變化,壓力的輕微增加會引起彎曲變形的明顯增大,表明柱已喪失承載能力。
設失穩前柱的軸線為理想直線,壓力作用線與軸線重合,材料服從胡克定律,且失穩后撓度很小,則細長柱臨界壓力的計算公式為:
式中E為材料的彈性模量,I為柱截面的形心主慣性矩(見截面的幾何性質),l為柱的長度;μ為和約束條件有關的係數,對兩端鉸支的柱,μ=1;對一端固定另一端自由的柱,μ=2。
L.歐拉曾給出一端固定另一端自由的柱的臨界壓力公式,即雖然歐拉未說明常數C的物理意義,但已提出柱的穩定概念並得出正確的公式。後人稱式(1)為歐拉公式,並把按式(1)算出的臨界壓力 稱為歐拉力,以柱的橫截面面積A除,即引入柔度λ僅與柱本身的幾何性質和約束條件有關,與載荷無關。上式取等號,可求出使應力不超過比例極限的最小柔度:
從而得到歐拉公式使用的範圍是:λ>λ1。
中長柱的非線彈性失穩
柔度小於λ1的柱,其應力往往在低於式(4)時,就已超過比例極限,因而往中開始出現塑性變形。但仍和細長彈性柱相似,在某一極限壓力下,柱的直線平衡狀態會由直線過渡為曲線。這一極限壓力也稱為臨界壓力。應力超過比例極限后的失穩稱為非線彈性失穩。計算非線彈性失穩臨界壓力的公式有多種,既有理論公式(如切線彈性模量公式和折減彈性模量公式),又有以大量實驗資料為基礎建立起來並在工程中得到普遍應用的經驗公式(如直線公式和拋物線公式等);
① 切線彈性模量公式 對兩端簡支的柱,切線彈性模量公式為:②折減彈性模量公式 對兩端簡支的柱,折減彈性模量公式為:式中Er稱為折減彈性模量,其值為:式中I1和I2分別為微彎變形中橫截面內壓縮區和拉伸區對中性軸(即壓縮區和拉伸區的分界線)的慣性矩。至於中性軸的位置則由下式確定:
式中S1和S2分別為壓縮區和拉伸區對中性軸的靜矩。
③直線公式和拋物線公式 這些公式都是根據實驗資料建立的經驗公式。直線公式把臨界應力和柔度λ表示為直線關係,即拋物線公式則把λ表示為拋物線關係,即以上兩式中常數a、b和a1、b1都是與材料有關的常數,應根據實驗資料確定。
短柱的強度破壞
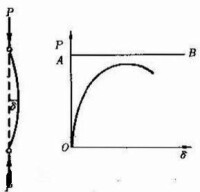
柱
上述結論中都假設柱的軸線為理想直線,壓力和軸線重合且材枓是均勻的。在這種理想情況下,當P
目錄
