阿伏加德羅定律
阿伏加德羅定律
阿伏加德羅定律(阿伏伽德羅定律及推論)(英文名:Avogadro's Hypothesis)主要說明:同溫同壓下,相同體積的任何氣體含有相同的分子數,稱為阿伏加德羅定律。
氣體的體積是指所含分子佔據的空間,通常條件下,氣體分子間的平均距離約為分子直徑的10倍,因此,當氣體所含分子數確定后,氣體的體積主要決定於分子間的平均距離而不是分子本身的大小。
阿伏加德羅定律(Avogadro's law)在相同的溫度和壓強下,相同體積的任何氣體都含有相同數目的分子。所以又叫四同定律,也叫五同定律或克拉貝隆方程(五同指同溫、同壓、同體積、同分子個數、同物質的量)。
理想氣體(即氣體分子無體積,各分子間無作用力。P.S:在高溫高壓下,許多氣體都接近於理想氣體),可以是單一氣體,也可以是混合氣體。可以是單質氣體,也可以是化合物氣體。
我們可以利用阿伏加德羅定律以及物質的量與分子數目、摩爾質量之間的關係得到以下有用的推論:
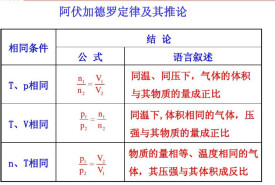
(1)同溫同壓時:①V1:V2=n1:n2=N1:N2 ②ρ1:ρ2=M1:M2 ③ 同質量時:V1:V2=M2:M1
(2)同溫同體積時:④ P1:P2=n1:n2=N1:N2 ⑤ 同質量時: P1:P2=M2:M1
(3)同溫同壓同體積時: ⑥ ρ1:ρ2=M1:M2=m1:m2
具體的推導過程請大家自己推導一下,以幫助記憶。推理過程簡述如下:
(1)、同溫同壓下,體積相同的氣體就含有相同數目的分子,因此可知:在同溫同壓下,氣體體積與分子數目成正比,也就是與它們的物質的量成正比,即對任意氣體都有V=kn;因此有V1:V2=n1:n2=N1:N2,再根據n=m/M就有式②;若這時氣體質量再相同就有式③了。
(2)、從阿伏加德羅定律可知:溫度、體積、氣體分子數目都相同時,壓強也相同,亦即同溫同體積下氣體壓強與分子數目成正比。其餘推導同(1)。
(3)、同溫同壓同體積下,氣體的物質的量必同,根據n=m/M和ρ=m/V就有式⑥。當然這些結論不僅僅只適用於兩種氣體,還適用於多種氣體。
克拉佩龍方程又稱“理想氣體方程式”。中學化學中,阿伏加德羅定律佔有很重要的地位。它使用廣泛,特別是在求算氣態物質分子式、分子量時,如果使用得法,解決問題很方便。下面簡介幾個根據克拉伯倫方程式導出的關係式,以便更好地理解和使用阿伏加德羅定律。
克拉佩龍方程通常用下式表示:PV=nRT……①
P表示壓強、V表示氣體體積、n表示物質的量、T表示絕對溫度、R表示氣體常數。所有氣體R值均相同。如果壓強、溫度和體積都採用國際單位(SI),R=8.31帕·米3/摩爾·開。如果壓強為大氣壓,體積為升,則R=0.082大氣壓·升/摩爾·度。
因為n=m/M、ρ=m/v(n—物質的量,m—物質的質量,M—物質的摩爾質量,數值上等於物質的分子量,ρ—氣態物質的密度),所以克拉佩龍方程式也可寫成以下兩種形式:
Pv=mRT/M……②和PM=ρRT……③
以A、B兩種氣體來進行討論。
(1)在相同T、P、V時:
根據①式:nA=nB(即阿伏加德羅定律)
分子量一定
摩爾質量之比=密度之比=相對密度。若mA=mB則MA=MB。
(2)在相同T、P、m時:
體積之比=摩爾質量的反比;兩氣體的物質的量之比=摩爾質量的反比。
物質的量之比=氣體密度的反比;兩氣體的體積之比=氣體密度的反比。
(3)在相同T·V時:
兩氣體的壓強之比=氣體分子量的正比=摩爾質量的反比。
我們可以利用阿伏加德羅定律以及物質的量與分子數目、摩爾質量之間的關係得到以下有用的推論:
(1)同溫同壓時:①V1:V2=n1:n2=N1:N2 ②ρ1:ρ2=M1:M2 ③ 同質量時:V1:V2=M2:M1
(2)同溫同體積時:④ P1:P2=n1:n2=N1:N2 ⑤ 同質量時: P1:P2=M2:M1
(3)同溫同壓同體積時: ⑥ ρ1:ρ2=M1:M2=m1:m2
具體的推導過程請大家自己推導一下,以幫助記憶。推理過程簡述如下:
(1)、同溫同壓下,體積相同的氣體就含有相同數目的分子,因此可知:在同溫同壓下,氣體體積與分子數目成正比,也就是與它們的物質的量成正比,即對任意氣體都有V=kn;因此有V1:V2=n1:n2=N1:N2,再根據n=m/M就有式②;若這時氣體質量再相同就有式③了。
(2)、從阿伏加德羅定律可知:溫度、體積、氣體分子數目都相同時,壓強也相同,亦即同溫同體積下氣體壓強與分子數目成正比。其餘推導同(1)。
(3)、同溫同壓同體積下,氣體的物質的量必同,根據n=m/M和ρ=m/V就有式⑥。當然這些結論不僅僅只適用於兩種氣體,還適用於多種氣體。
在同溫同壓下,像在上面結論式②和式⑥中出現的密度比值稱為氣體的相對密度D=ρ1:ρ2=M1:M2。
注意:①.D稱為氣體1相對於氣體2的相對密度,沒有單位。如氧氣對氫氣的密度為16。
②.若同時體積也相同,則還等於質量之比,即D=m1:m2。
阿伏加德羅定律推論
阿伏加德羅定律及推論都可由理想氣體狀態方程及其變形推出(壓強、體積、絕對溫度、物質的量、氣體常數、密度)。由定律可導出:“一連比、三正比、三反比”的規律。
1.“一連比”:指在同溫同壓下,同體積的任何氣體的質量比等於摩爾質量(相對分子質量)之比,等於密度比。
2.“三正比”
(1)同溫同壓下,兩氣體的體積之比等於其物質的量之比,等於其分子數之比。
(2)同溫同體積下,兩氣體的壓強之比等於其物質的量之比,等於其分子數之比。
(3)同溫同壓下,兩氣體的密度之比等於其摩爾質量(又稱相對分子質量)之比。
3.“三反比”
(1)同溫同壓同質量下,兩氣體的體積與其摩爾質量(相對分子質量)成反比。
(2)同溫同分子數(或等物質的量)時,兩氣體的壓強與其體積成反比。
(3)同溫同體積同質量下(同密度時),兩氣體的壓強與其摩爾質量(相對分子質量)成反比。