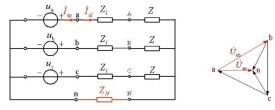
對稱三相電路
電路系統之一
三相電路就是由對稱三相電源和三相負載聯接起來所組成的系統,本質上依然是正弦交流電路。工程上根據實際需要,可以組成Y-Y聯接方式,Y-△聯接方式,還有△-Y和△-△聯接方式,不同連接方式可以等效替換,但電路參數的關係互不相同。當組成三相電路的電源和負載都對稱時,就稱為對稱三相電路。
對稱三相電路和對稱三相負載相連接,稱為對稱三相電路(一般情況下,電源總是對稱的)。三相電源與負載之間的連接方式有Y-Y,△-Y,△-△,Y-△連接方式。三相電路實際是正弦交流電路的一種特殊類型。在三相電路中,三相負載的連接方式決定於負載每相的額定電壓和電源的線電壓。由於對稱三相電路中每組的響應都是與激勵同相序的對稱量。所以,每相不但相電壓有效值相等,相電流有效值也相等。而且每相電壓與電流的相位差也相等。從而每相的有功功率相等。
Δ連接與Y連接
三相電路中,電源(電壓源或電流源)與負載均為三相,三相之間存在兩種連接方式,分別為Δ(三角)接法與Y(星型)接法,電源與負載的接法並不要求統一,兩種接法之間可以相互等效變換。但是不同的接法,電路中的參數關係互不相同。
Δ連接與Y連接在三相電路中起著不同的作用,Δ連接能使得三倍頻諧波在閉環內形成環流,避免三倍頻諧波對電路的影響,採用Y連接並使得中性點接地時,可以使得零序電路構成通路,在電纜以及長距離三相高壓輸電的繼電保護中起著零序保護的關鍵作用。
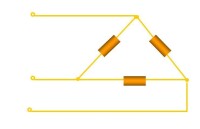
三角形接法
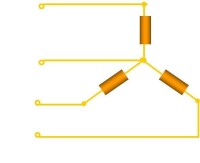
星型接法
線電壓與相電壓
電壓定義為電路中某一點與參考點之間的電勢差,對於單相電路,電壓參考點為地,對於三相電路,電壓參考點選取為地時,每相上的電壓稱為相電壓,若電壓參考點選取為相,則相與相之間的電壓稱為線電壓。當三相電路的Y接法中性點不接地,或採用Δ接法時,相電壓往往難以測量,此時採用線電壓反而更為直接。
對稱三相電路
對於Δ接法,線電壓大小等於相電壓,相位相同。
線電流與相電流
類似於相電壓與線電壓的定義,定義流過某一相的電流為相電流,定義兩相之間的電流差為線電流,則對於堆成三相電路
採用Y接法,線電流等於相電流,相位相同。
對稱三相電路
Y-Δ變換
Y接法和Δ接法可以根據分析需求進行相互之間的等效變換,其簡要推導過程如下
對於Y接法與Δ接法的電路
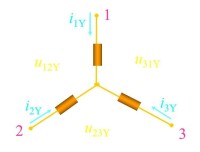
Y接法
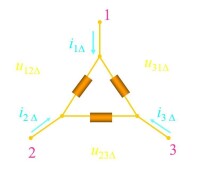
Δ接法
其等效條件為替換前後,每個負載兩端電壓與流經電流不變,結合兩者的VCR,可以得到
Y-Δ變換公式
對稱三相電路
對稱三相電路
對稱三相電路
Δ-Y變換公式
對稱三相電路
對稱三相電路
對稱三相電路
對稱分量法與單相等值電路
早在1918年,福蒂斯丘(Fortescue)提出了對稱分量法,基於電力網路各元件參數對稱的前提下,對稱分量法可以將故障網路分解為正、負、零三序相互解耦的網路,為故障分析計算提供了極大方便。對於對稱三相電路,可以視為零序分量與負序分量均為零,僅存在正序分量的特殊堆成分量電路。
單相等值電路需要公共端(中性點)相連,要求中性點電壓為零,而所說的中性點也即“零電位點”,或者所謂的“地”。單相等值電路是基於三相元件參數完全對稱,三相電流、電壓完全對稱的條件下得到的。它以無窮遠處為零電位點,並且計及另外兩相的影響之後得到以零電位點為公共端的單相等值電路。利用星形等值法,即將電源、變壓器和負載都等值為星形連接,當系統完全對稱時,就可以直接把中性點N和n用一根導線連接起來。由於三相對稱,各相相角相差120°,就可以選擇其中一相來計算。
但是單相等值電路分析法有其不足之處,首先,單相等值電路是基於系統三相電氣量、網路參數完全對稱的,這與現代電力系統相參數越來越不對稱的狀況以及運行狀況導致的不對稱等等情況不相符合。當系統參數不對稱時,系統內各個中性點電壓不相等也不為零,即存在中性點電壓偏移,三相電壓不對稱,這就導致不能用單相等值電路代替三三相等值電路;因為系統參數的不對稱,使得正常運行和故障時中性點電壓偏移,危害中性點設備,引起中性點絕緣等問題,有必要對變壓器中性點電壓進行分析,確定保護方案以及中性點接地方式配置問題。
電力系統中,中性點接地方式複雜多樣,有必要尋找種更加精確、更加符合運行實際的等值電路描述中性點接地信息。變壓器用單相等值電路不能表達其原副邊的相位移,必須做變換才能得到實際相位,
在故障計算中通常略去非故障相的電流,即非故障相開路,這可能會造成遠離故障點處的計算電壓與實際電壓偏移很大。
即使如此,單相等值電路分析法依然在對稱三相電路分析中有著舉足輕重的地位。這是因為三相對稱電路中,三相參數均對稱,取一相進行分析,可以大幅簡化計算,並且可以很方便地求解電路功率等參數。