等角對等邊
等角對等邊
在同一三角形中，如果兩個角相等，那麼這兩個角所對的邊也相等。通常用來證明等腰三角形。（等邊對等角的逆定理)
等角對等邊的性質在人教版八年級上冊數學第十五章《軸對稱》有所學習。
在同一三角形中，如果兩個角相等，那麼這兩個角所對的邊也相等。通常證明等腰三角形。（等邊對等角的逆定理)
英文名稱(sides opp. equal angles)
等角對等邊的性質在人教版八年級上冊數學第十二章《軸對稱》有所學習。
“等角對等邊”性質
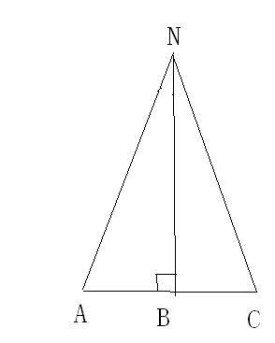
證明：∵ NB⊥AC（已知）
∴ ∠NBA=∠NBC=90°（垂直定義）
在△NBA和△NBC中， ∠NBA=∠NBC（已證）
∠A=∠C（已知）
NB=NB（公共邊）
∴△NBA≌△NBC（AAS）
∴NA=NC（全等三角形的對應邊相等）
如圖，NB平分∠ANC，∠A=∠C，求證：NA=NC
證明：∵NB平分∠ANC（已知），
∴∠ANB=∠CNB
在△ANB和△CNB中，
∠ANB=∠CNB（已證）
∠A=∠C（已知）
NB=NB（公共邊）
∴△ANB≌△CNB（AAS）
∴NA=NC（全等三角形的對應邊相等）
（歐幾里德《幾何原本》命題6）
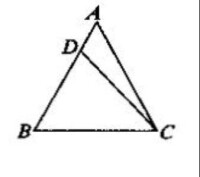
等角對等邊
則可證邊AB等於邊AC
若AB不等於AC，其中必有一個較大，設AB是較大的；
由AB上截取DB等於較小的AC，連接DC
那麼，DB等於AC且BC公用，兩邊DB、BC分別等於邊AC、CB，
且角DBC等於角ACB
所以，底BC等於底AB，且三角形DBC全等於三角形ACB，即小的等於大的；
這是不合理的。
所以，AB不能不等於AC，從而它等於它。
證完
無需作線
∠A=∠C（已知）
∠C=∠A（已知）
AC = CA （公共邊）
∴△NAC≌△NCA（AAS）
∴NA=NC（全等三角形的對應邊相等）
∵∠A=∠C
∴sinA=sinC
∵NA/sinC=NC/sinA（正弦定理）
∴NA=NC
基本信息
- 中文名
- 等角對等邊
- 外文名
- sides opp. equal angles
- 別名
- 軸對稱
- 應用學科
- 數學
- 學習
- 人教版八年級上冊數學