光度

謂“”，指恆星形式輻射功率。恆星溫低。般，恆星溫越低，越偏紅；溫越，則越偏藍。溫越，積越，越。恆星顏，科提取息。恆星秒量值。決項素：龐恆星具較積，具較溫，故較。

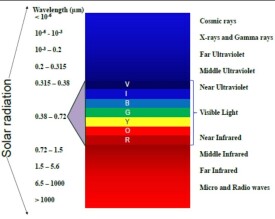
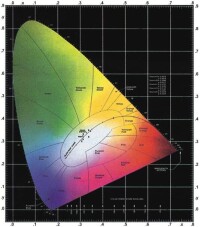
顆恆星秒鐘輻射量。波磁輻射量示，熱；則指某波範圍輻射。溫(顏)顆恆星極，顆恆星完溫(顏)。

源發光強度和光線在物體表面的照度以及物體表面呈現的亮度的總稱（光源發光強度和照射距離影響照度；照度大小和物體表面色澤影響亮度）。在攝影中，光度與曝光直接相關。從構圖上來說，曝光與影調或色彩的再現效果密切相關。豐富的影調和準確的色彩再現是以準確曝光為前提的。有意識的曝光過度與不足也需以準確曝光為基礎。所以，掌握光度與準確曝光的基本功，才能主動地控制被攝體的影調、色彩以及反差效果。

攝影所用光源無外兩種，其一是自然光源，即從太陽的照射而獲得；其二是人造光源，即各種照相所用燈光。

天文學中指恆星或其他天體單位時間發出的輻射能量。

在光度學(photometry)中，“光度”是發光強度在指定方向上的密度，但經常會被誤解為照度。照度的國際單位是每平方米所接受的燭光(中國大陸、港澳稱坎德拉)。

在天文學中，光度是物體每單位時間內輻射出的總能量。在國際單位的典型表示法式是瓦特(Watt)，在c.g.s.制是爾格/秒，或是以太陽光度來表示，也就是以太陽輻射的能量為一個單位來表示。太陽的光度是瓦特。

恆星光度決定於兩項因素：龐大的恆星具有較大的表面面積去發出光能，因此光度較大。熱恆星具有較高的表面溫度，故發出較多光能，因此光度也是較大。例如：具有較大表面面積的熱恆星一定很亮；具有較小表面面積的冷恆星一定很暗，但是具有非常大表面面積的冷恆星卻可以很光亮。

光度是與距離無關的真實獨立常數，亮度則明顯的與距離有關，而且是與距離的平方成反比，亮度通常會以視星等來量度，那是一種對數的關係。

在測量恆星的亮度時，光度、視星等和距離是相關的參數。如果你已經知道其中的兩項，就可以算出第三項。因為太陽的光度是一個標準值，以太陽的視星等和距離做為這些參數的比較標準，就很容易完成彼此之間的轉換。

光度和亮度之間的計算

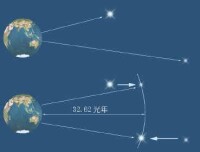
假設是一個點光源的光度，他向四周輻射的能量是均等的。這個點光源被安置在一個中空球殼的中心，則輻射的所有能量都將穿過這個球殼。當半徑增加時，球殼的表面積也將增加，但通過球殼的光度是恆定不變的，所以將導致在球殼上觀察到的亮度下降，此處是被照亮的球殼表面積。對恆星和一個點光源而言，所以，此處是點光源與觀測者的距離。

對一顆主序星，光度也與質量相關，這就很容易知道恆星的光度、溫度、半徑和質量之間都是有關聯的。

恆星的星等與亮間是對數的關係，視星等是從地球上觀察到的亮度，絕對星等是在10秒差距上的視星等。只要知道光度，我們就可以計算在任一給定距離上的視星等：一顆熱星等為−10的明亮恆星的光度是106，而熱星等+17等星的暗星光度是10−5。注意絕對星等可以直接與光度對應，但視星等則是距離的函數。因為只有視星等可以經由觀測直接測量，而有了估計的距離才能確定目標的光度。

攝影中的光度是指物體的表面受光源的照射所呈現出的亮度。光度與光源種類、性質及發光強度、照射距離和被攝物表面的物理特性對光線的反射能力的大小密切相關。

攝影所用光源無外兩種，其一是自然光源，即從太陽的照射而獲得；其二是人造光源，即各種照相所用燈光。

太陽光的強度為一恆值，但照度多變，它隨四季、天氣狀況、時辰、海拔高度、地理緯度、經度的變化而發生改變。而人造光源一旦設定，其強度也不改變。但與距離遠近關係密切，即距離愈近，照度越強；距離愈遠，照度越弱。

了解並深諳光度的特性，對於拍好每一張照片很有幫助。特別提示影友，在兩種光源同用時拍攝，要特別注意兩種光源的反差問題。據相關資料介紹，2千瓦鎢絲燈在距離光源1米時的照度大致相當於平原地區春秋季節，中午晴天條件下的太陽照度。

在散射理論和加速器，光度是在單位時間內在標靶的單位面積上所吸收的粒子數目，在cgs單位制下的因次為公分-2秒-1或b-1s-1，光度的累積是光度對時間的積分。光度是描述加速器性能和特性的重要數值。

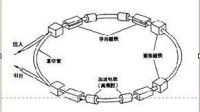
與光度有關的元素

L是光度

N是參與互動的數目。

ρ是在每一束粒子束內的粒子密度。

σ是全部的有效截面積。

dΩ是微分的立體角。

是微分的有效截面積。

於是有下列的關係存在：

(如果標靶是理想的非導體)

對一個相交的儲存環對撞機：

f是交流頻率

n是在儲存環上的每個良上的線圈數。

Ni是每一束中的粒子數目。

A是粒子束的截面積。

愛丁頓光度是吸積天體所能達到的最大光度。天體在吸積周圍介質的同時發出輻射，當吸積物質累積到一定程度，輻射壓會阻止物質的進一步下落。此時天體作用在一個粒子上的引力與其受到的輻射壓力達到平衡。天體吸積所能達到的光度與其自身質量成正比，並且太陽的愛丁頓光度是其光度的104倍。一般說來，普通恆星的光度遠遠低於愛丁頓光度，某些X射線雙星和活動星系核的光度能夠達到愛丁頓光度，伽瑪射線暴、超新星爆發可以在短時間內超過愛丁頓光度。