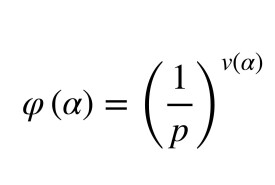離散賦值

當一階賦值φ的值群為無限循環群時，則φ稱為離散賦值。

例如，關於有理數域Q。設p是一個素數，那麼每個有理數α≠0都可惟一地寫成 的形式，其中b、с是與p互素的整數，v(α)∈Z。規定，以及φ(0)=0。不難驗知，φ滿足賦值的條件，而且是一個離散賦值，稱之為Q的p進賦值。

【discrete valuation ring】

設(R，m)是一個維數為1的諾特局部環，如果m可以由一個元素生成，則稱R是離散賦值環。

離散賦值環一定是整環。

設(R，m)是一個維數為1的諾特局部整環，則下列條件等價：

（1）R是離散賦值環；

（2）R的每個非零理想都是m的一個方冪；

（3）存在a∈R使得R的每個非零理想都具有形式(aᵏ)，k≥0。

離散賦值環對應於離散賦值。假設R是離散賦值環，F是R的商域。令

這裡， 。則是F的一個離散賦值。

例如，設p是素數，則 是離散賦值環。