切映射是一種可微映射。微分流形之間的可微映射誘導出它們的切叢之間可微映射。
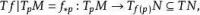
切映射
設f:M→N是微分流形M到N的可微映射,Tf:TM→TN,使得對於p∈M,其中f是f在p∈M處的微分。此時稱Tf是f的切映射。
若記π:TM→M,π:TN→N均為叢射影,則f∘π=π∘Tf。
若f:M→N是微分同胚映射,則Tf:TM→TN亦然。因此,切叢是流形在微分同胚下保持不變的重要性質。

切映射
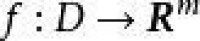
切映射
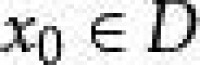
切映射
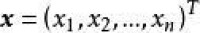
切映射
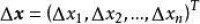
切映射
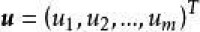
切映射
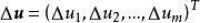
切映射
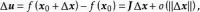
切映射
切映射
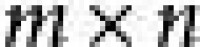
切映射
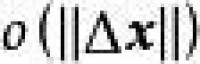
切映射

切映射
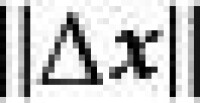
切映射
切映射
切映射
設D是 中的一個區域,是以D為定義域的映射, ,如果對於
自變數 的增量,
因變數 的增量 可以分解為 其中 是一個 陣,是m維空間 中的向量,它的各分量均是比 高階的無窮小量,則稱映射 在 點 可微。