四種命題
四種命題
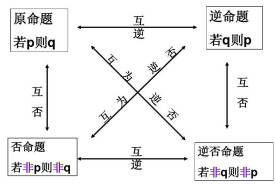
四種命題包括原命題、逆命題、否命題和逆否命題。
有個人請客辦事,看看約定的時間過了,還有一大半的客人沒來。主人心裡很焦急,便說:“怎麼搞的,該來的客人還不來?”一些敏感的客人聽到了,心想:“該來的沒來,那我們是不該來的嘍?”於是悄悄地走了。
主人一看又走掉好幾位客人,愈發著急了,便說:“怎麼這些不該走的客人,反倒走了呢!”剩下的客人一聽,又想:“走了的是不該走的,那我們這些沒走的倒是該走的了!”於是又都走了。
最後只剩下一個跟主人較親密的朋友,看到這種尷尬的場面,就勸他說:“你說話前應該先考慮一下,否則說錯了,就不容易收回來了。”
主人大叫冤枉,急忙解釋說:“我並不是想讓他們走的啊!”這個朋友聽了,大為光火,說:“不是叫他們走,那就是叫我走了!”說完,頭也不回地離開了。
四種命題
1、對於兩個命題,如果一個命題的條件和結論分別是另外一個命題的結論和條件,那麼這兩個命題叫做互逆命題,其中一個命題叫做原命題,另外一個命題叫做原命題的逆命題。
2、對於兩個命題,如果一個命題的條件和結論分別是另外一個命題的條件的否定和結論的否定,那麼這兩個命題叫做互否命題,其中一個命題叫做原命題,另外一個命題叫做原命題的否命題。
3、對於兩個命題,如果一個命題的條件和結論分別是另外一個命題的結論的否定和條件的否定,那麼這兩個命題叫做互為逆否命題,其中一個命題叫做原命題,另外一個命題叫做原命題的逆否命題。
1、四種命題的相互關係:原命題與逆命題互逆,逆命題與逆否命題互否,逆否命題與否命題互逆,否命題與原命題互否,原命題與逆否命題相互逆否,逆命題與否命題相互逆否。
2、四種命題的真假關係:
(1)兩個命題互為逆否命題,它們有相同的真假性。
(2)兩個命題為互逆命題或互否命題,它們的真假性沒有關係。
1、階下之囚
“我真發愁”監獄看守員說,“警察帕金斯留了個條子說,昨晚他逮捕了兩個牧師打扮的流氓。但我今早上班時卻發現一共有三個牧師打扮的人,現在看來其中有一名是個真正的牧師,他是前來探望兩個誤入歧途的‘羔羊’的,問題是我現在分不清誰真誰假了。”
“這有何難?想辦法問問他們嘛”警官建議,“真人不說假話,真正的牧師一定是講真話的。”
“你說的到不錯,但我也許正好問到那個騙子呢?帕金斯說過,這傢伙是個撒謊老手,從不講真話。而那個賭棍則是個見風使舵的傢伙,他說起話來,時真時假,要看形勢對他是否有利而定。”
警官走到單人牢房前。
“你是誰?”他問一號牢房裡的囚犯。
“我是賭棍。”其人答道。警官又走到二號牢房前問:
“一號牢房裡關著的那個人是誰?”
“騙子!”
警官又問三號牢房裡的人:“你說一號牢房裡的那個人是誰?”
三號牢房裡的人答道:“牧師。”
警官轉身對看守員說:“很明顯,你應該釋放------”
該放誰?
2、誰即可要火腿,又可要豬排?
四種命題
安、布和卡三人去餐館吃飯,他們每人要的不是火腿就是豬排。
1、如果安要的是火腿,那麼布要的就是豬排。
2、安或卡要的是火腿,但是不會兩人都要火腿。
3、布和卡不會兩人都要豬排。
問:誰即可以要火腿,又可以要豬排?
3、醫務人員

四種命題
(1)護士多於醫生。
(2)男醫生多於男護士。
(3)男護士多於女護士。
(4)至少有一位女醫生。”
這位說話的人是什麼性別和職務?
4、弗里曼先生的未婚妻
弗里曼先生認識埃達、比、茜德、黛布、伊芙這五位女士。
(1)五位女士分為兩個年齡檔:三位女士小於30歲,兩位女士大於30歲。
(2)兩位女士是教師,其他三位女士是秘書。
(3)埃達和茜德屬於相同的年齡檔。
(4)黛布和伊芙屬於不同的年齡檔。
(5)比和伊芙的職業相同。
(6)茜德和黛布的職業不同。
(7)弗里曼先生將同其中一位年齡大於30歲的教師結婚。
誰是弗里曼先生的未婚妻?
提示:確定哪幾位女士的年齡小於30歲,哪幾位女士是秘書。
5、分別是哪國人?

四種命題
現已知:
(1)A和美國人是醫生;
(2)E和俄羅斯人是教師;
(3)C和德國人是技師;
(4)B和F曾經當過兵,而德國人從沒當過兵;
(5)法國人比A年齡大,義大利人比C年齡大;
(6)B同美國人下周要到英國去旅行,C同法國人下周要到瑞士去度假。
請判斷A、B、C、D、E、F分別是哪國人?
6、誰是罪犯?
對某盜竊案三位嫌疑犯來說,下列事實成立,問誰是罪犯?
(1)A、B、C中至少有一人有罪。
(2)A有罪時,b、c與之同案。
(3)C有罪時,A、B與之同案。
(4)B有罪時,沒有同案者。
(5)A、C中至少有一人無罪。
7、誰說謊?

四種命題
張三:李四說謊。
李四:王五說謊。
王五:張三李四都說謊。
問:誰說謊,誰沒說謊?
命題邏輯學簡易邏輯集合數學邏輯聯結詞等價
[2]、《測試你的邏輯推理能力》 美. 喬治薩默斯 著 林自新 譯 上海科技教育出版社
[3]、IQ超人網 http://www.iqsuperman.net/index.php