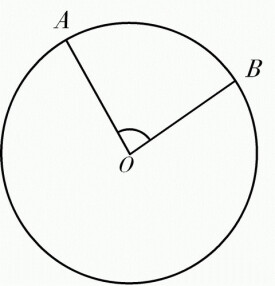
圓心角

定理

圓心角的度數等於它所對的弧的度數。

與弧、弦、弦心距的關係

在同圓或等圓中，若兩個圓心角、兩條弧、兩條弦、兩條弦的弦心距中有一組量相等，則對應的其餘各組量也相等。

理解：(定義）

(1)等弧對等圓心角

(2)把頂點在圓心的周角等分成360份時，每一份的圓心角是1°的角．

(3)因為在同圓中相等的圓心角所對的弧相等，所以整個圓也被等分成360份，這時，把每一份這樣得到的弧叫做1°的弧．

(4)圓心角的度數和它們對的弧的度數相等．

推論：

在同圓或等圓中，如果(1)兩個圓心角,(2)兩條弧,(3)兩條弦(4)兩條弦上的弦心距中，有一組量相等，那麼它們所對應的其餘各組量都分別相等

與圓周角關係

在同圓或等圓中，同弧或同弦所對的圓周角等於二分之一的圓心角。

定理證明：證明。

作直徑CD，

∵OA = OB = OC

∴∠OBC = ∠OCB ∠OAC = ∠OCA

∴∠BOD = ∠OBC+∠OCB = 2∠BCD

即：∠BCD = 1/2∠BOD

同理：∠ACD = 1/2∠AOD

∴∠ACB = ∠BCD - ∠ACD

= 1/2（∠BOD - ∠AOD）

= 1/2∠AOB

①L(弧長)=(r/180)XπXn（n為圓心角度數，以下同）；

②S(扇形面積) = (n/360)Xπr；

③扇形圓心角n=（180L）/（πr）（度）。

④K=2Rsin(n/2) K=弦長；n=弦所對的圓心角，以度計。

①頂點是圓心；

②兩條邊都與圓周相交。

③圓心角性質：在同圓或等圓中，相等的圓心角所對的弧相等，所對的弦相等，所對的弦的弦心距也相等。在同圓或等圓中，圓心角、圓心角所對的弦、圓心角所對的弧和對應弦的弦心距，四對量中只要有一對相等，其他三對就一定相等。

④一條弧的度數等於它所對的圓心角的度數。

⑤半圓（或直徑）所對的圓周角是直角；90°的圓周角所對的弦是直徑。