優選法
優選法
優選法,(optimization method),以數學原理為指導,合理安排試驗,以儘可能少的試驗次數儘快找到生產和科學實驗中最優方案的科學方法。即最優化方法。
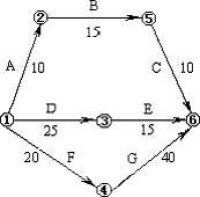
優選法
優選法,是指研究如何用較少的試驗次數,迅速找到最優方案的一種科學方法。例如:在現代體育實踐的科學實驗中,怎樣選取最合適的配方、配比;尋找最好的操作和工藝條件;找出產品的最合理的設計參數,使產品的質量最好,產量最多,或在一定條
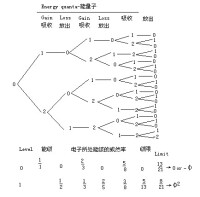
優選法
實際工作中的優選問題,即最優化問題,大體上有兩類:一類是求函數的極值;另一類是求泛函的極值。如果目標函數有明顯的表達式,一般可用微分法、變分法、極大值原理或動態規劃等分析方法求解(間接選優);如果目標函數的表達式過於複雜或根本沒有明顯的表達式,則可用數值方法或試驗最優化等直接方法求解(直接選優)。
優選法是儘可能少做試驗,儘快地找到生產和科研的最優方案的方法,優選法的應用在我國從70年代初開始,首先由我們數學家華羅庚等推廣並大量應用,優選法也叫最優化方法。
怎樣用較少的試驗次數,打出最合適的訓練量,這就是優選法所要研究的問題。應用這種方法安排試驗,在不增加設備、投資、人力和器材的條件下,可以縮短時間、提高質量,達到增強體質.迅速提高運動成績的目的。
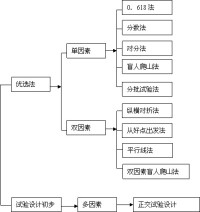
優選法
2)優化判據與影響因素直接的關係稱為目標函數。
3)優化計算。優化(選)試驗方法一般分為兩類:
分析法:同步試驗法
黑箱法:循序試驗法
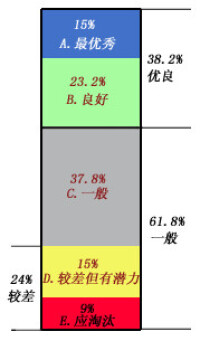
優選法
1.單因素優選法
如果在試驗時,只考慮一個對目標影響最大的因素,其它因素盡量保持不變,則稱為單因素問題。一般步驟:
(1)首先應估計包含最優點的試驗範圍,如果用a表示下限,b表示上限,試驗範圍為[a,b];
(2)然後將試驗結果和因素取值的關係寫成數學表達式,不能寫出表達式時,就要確定評定結果好壞的方法。
2.多因素優選法
多因素問題:首先對各個因素進行分析,找出主要因素,略去次要因素,划“多”為“少”,以利於解決問題。
單因素優選法解決的問題是針對函數在區間上有單峰極大值(或者極小值)。如何通過更加有效的選點方法縮小極值點的範圍。
在(a,b)區間內取兩點x1,x2。顯然:
1)當f(x1)>f(x2)時,極大點在(a,x2)的範圍內,(x2,b)的區間可以捨去。
2)當f(x1)
3)當f(x1)=f(x2)時,極大點在(x1,x2)的範圍內,(a,x1),(x2,b)的區間可以捨去。每次捨棄完一定的區間后,在剩餘的點中需要重新找點,迭代計算。
即第一次循環,需要找到x1,x2,並且計算f(x1),f(x2)
第二次循環,需要找到x3,x4,並且計算f(x3),f(x4)但是刪除的區間可能是某個實驗點到上下限的範圍,則另一個實驗點如果能夠重用,將非常減少計算量。
0.618法就是採用這樣的思路:第一次選擇0.382(b-a),0.618(b-a),若保留了(0,0.618),由於0.618*0.618=0.382,因此下一輪只需要在0.618*0.382=0.216處實驗,0.382的實驗結果在上一輪中得出,減少了計算量,每次消去的區間還大。
除此之外,針對參數只能取整數的優選可以採用Fibonacci優選。在(a,b)區間分成等分,問題變為在(0,)範圍內求極值。第一次選擇和,若保留下的區間是(0,),則下次只需要計算,已經在上次迭代中計算過。若可參加實驗的點數有限固定在一定範圍,可以通過添加新的無關點來湊足Fibonaac數列。無關點即為比其他實驗點都差的點。
目錄
