耦合電感
耦合電感
電感元件也稱為自感元件,如果兩個或兩個以上的線圈中每個線圈所產生的磁通都與另一個線圈相交鏈,則稱這些線圈有磁耦合(magnetic coupling)或者說具有互感(mutual induction)。若假定這些線圈是靜止的,並且忽略了線圈中的電阻和匝間的分佈電容,具有磁耦合的諸線圈就可表示為理想化的耦合電感元件(coupled inductor),簡稱耦合電感。
耦合電感
耦合電感
耦合電感
若兩個線圈的磁場存在相互作用,則稱這兩個線圈 磁耦合。如表1所示為具有磁耦合的兩個線圈,線圈1和2的匝數分別為,電感為。在表1(a)中,當施感電流 流入線圈1時,在線圈1中產生
耦合電感
耦合電感
耦合電感
耦合電感
耦合電感
耦合電感
耦合電感
耦合電感
耦合電感
耦合電感
耦合電感
,自感磁鏈。的一部分或全部交鏈線圈2時,在線圈2中產生互感磁通,互感磁鏈。在表1(b)中,當施感電流 流入線圈2時,在線圈2中產生自感磁通,自感磁鏈。的一部分或全部交鏈線圈1時,在線圈1中產生互感磁通,互感磁鏈。
如果線圈周圍的媒質為非鐵磁物質時,自感磁鏈為
耦合電感
耦合電感
耦合電感
耦合電感
耦合電感
耦合電感
耦合電感
式(2)中,和 稱為互感係數,簡稱互感,單位為亨(H)。可以證明, ,略去M的下標,常用M來表示兩個耦合線圈的互感。從而,當 和 同時流入線圈1和2時,如表1(c)所示,則線圈1和2的磁鏈取自感磁鏈方向,此時分別有
耦合電感
| 表1 具有磁耦合的兩個線圈 | ||
|---|---|---|
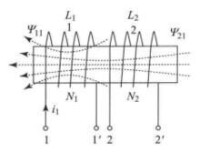 圖(a) | 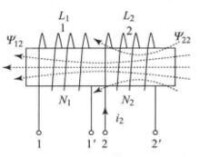 圖(b) | 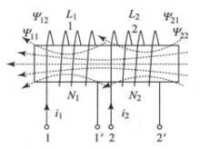 圖(c) |
耦合電感
耦合電感
耦合電感
耦合電感
耦合電感
一個線圈上互感磁鏈和自感磁鏈的方向不一定是相同的。如表2(a)所示,流出線圈2的端子2時互感磁鏈 與自感磁鏈 方向相反;如表2(b)所示,線圈2的繞向與線圈1的繞向相反時互感磁鏈 與自感磁鏈 方向相反。此時有
耦合電感
| 表2 磁鏈的方向 | |
|---|---|
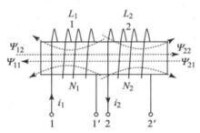 圖(a) | 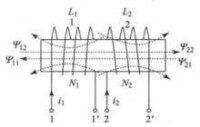 圖(b) |
耦合電感
耦合電感
耦合電感
耦合電感
耦合電感
耦合電感
耦合電感
耦合電感
耦合電感
耦合電感
設線圈上 與、與 取關聯參考方向,與、 ,和 與、符合右手螺旋定則。由電磁感應定律,可得
耦合電感
耦合電感
耦合電感
式(4)中,為自感電壓,為互感電壓。由式(3)和式(4)可知,一個線圈上互感磁鏈與自感磁鏈方向相同時,互感電壓前取正號;相反時取負號。
在正弦穩態電路中,式(4)可寫為
耦合電感
耦合電感
耦合電感
式(5)中,稱為互感抗,記為。
同名端
耦合電感
耦合電感
耦合電感
耦合電感
耦合電感
耦合電感
耦合電感
耦合電感
耦合電感
耦合電感
式(4)中,互感電壓前取正負號取決於一個線圈上互感磁鏈與自感磁鏈的方向,而其不僅與電流的參考方向有關,還與兩線圈的繞向有關。由於實際線圈是密封的,難以知其繞向;即使知其繞向,在電路圖中畫出線圈繞向也不方便。為此引入同名端的概念,把通入兩電流時能使一個線圈上互感磁鏈與自感磁鏈同向的這兩個端子稱為 同名端,並用“ ·”或“*”等表示。如表1(c)中,流入線圈1的端子1,產生 和;流入線圈2的端子2,產生 和,與 (或 與 )同方向,故通入兩電流的端子1和2為同名端。
同名端的判斷
耦合電感
耦合電感
耦合電感
耦合電感
耦合電感
耦合電感
由於 和 同方向,和 同方向,故通入兩電流時各自所產生的磁通同向時,通入電流的這兩個端子就是同名端,反之為異名端。如表22(b),流入線圈1的端子1,流入線圈2的端子2,各自所產生的磁通反向,故端子1和2為異名端,即1和2 '為同名端表1(c)和表2(b)所示線圈分別可用表3(a)和(b)所示電路表示。
用同名端確定互感電壓的極性
耦合電感
耦合電感
標定同名端后就可方便地確定互感電壓的極性。由同名端定義,兩電流流入同名端,一個線圈上互感磁鏈與自感磁鏈同向,式(4)中互感電壓前取正號,因此,電流流進同名端,則在具有磁耦合的另一線圈的同名端上互感電壓為正極性。如圖1所示,流入同名端1,則互感電壓 在同名端2上為正極性,即
耦合電感
耦合電感
耦合電感
耦合電感
耦合電感
耦合電感
耦合電感
這樣,當 與、與 取關聯參考方向,和 取同名端為正極性時,自感電壓和互感電壓在同名端上都是正極性,式(4)中互感電壓就取正號了。
| 表3 用同名端表示的電路 | |
|---|---|
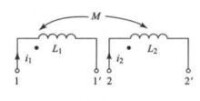 圖(a) | 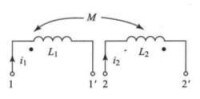 圖(b) |
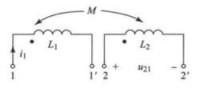
圖1 用同名端確定互感電壓的極性