半序
半序
半序一種條件較通常序弱的序關係。滿足自反性,傳遞性,反對稱性。
目錄
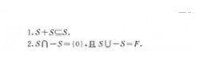
半序
因此,域F的一個半序實際上是加群F的一個序所決定的正元素集合。對於域,有實際意義的一種半序是所謂的T半序,這裡T是域F的一個亞正錐。域F的一個半序S,若T·SOS,則稱S為T半序;一個T半序S,若lES,則稱S為規範的。亞序域(F,T)的每個序都是規範的T半序,但反之未必。若域F的每個規範的T半序都是F的序,則稱T是一個帕施正錐或帕施序。當T是域F的弱亞正錐S;時,規範的S;半序稱為二次半序或q半序;且當S;是帕施正錐時,稱F是一個帕施域。二次半序(q半序)源於所謂的無帕施公理幾何,並在二次型理論中有應用意義.