矩陣乘法
一般矩陣乘積
矩陣相乘最重要的方法是一般矩陣乘積。它只有在第一個矩陣的列數(column)和第二個矩陣的行數(row)相同時才有意義。一般單指矩陣乘積時,指的便是一般矩陣乘積。一個m×n的矩陣就是m×n個數排成m行n列的一個數陣。由於它把許多數據緊湊的集中到了一起,所以有時候可以簡便地表示一些複雜的模型,如電力系統網路模型。
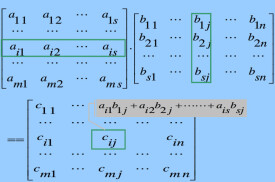
設A為的矩陣,B為的矩陣C為矩陣A與B的乘積,記作,其中矩陣C中的第行第列元素可以表示為:
如下所示:
1、當矩陣A的列數(column)等於矩陣B的行數(row)時,A與B可以相乘。
2、矩陣C的行數等於矩陣A的行數,C的列數等於B的列數。
3、乘積C的第m行第n列的元素等於矩陣A的第m行的元素與矩陣B的第n列對應元素乘積之和。
● ● 乘法結合律: (AB)C=A(BC).
● ● 乘法左分配律:(A+B)C=AC+BC
● ● 乘法右分配律:C(A+B)=CA+CB
● ● 對數乘的結合性k(AB)=(kA)B=A(kB).
● ● 轉置 (AB)=BA.
● ● 矩陣乘法一般不滿足交換律。
除了上述的矩陣乘法以外,還有其他一些特殊的“乘積”形式被定義在矩陣上,值得注意的是,當提及“矩陣相乘”或者“矩陣乘法”的時候,並不是指代這些特殊的乘積形式,而是定義中所描述的矩陣乘法。在描述這些特殊乘積時,使用這些運算的專用名稱和符號來避免表述歧義。
矩陣與矩陣的Hadamard積記作。其元素定義為兩個矩陣對應元素的乘積的m×n矩陣。例如,
克羅內克積是兩個任意大小的矩陣間的運算,符號記作。克羅內克積也被稱為直積或張量積。以德國數學家利奧波德·克羅內克命名。計算過程如下例所示:
C++代碼
struct Matrix:vector >//使用標準容器vector做基類,需#include語句{ Matrix(int x=0,int y=0,int z=0)//初始化,默認為0行0列空矩陣 { assign(x,vector(y,z)); } int h_size()const//常量說明不可省,否則編譯無法通過 { return size(); } int l_size()const { return empty()?0:front().size();//列數要考慮空矩陣的情況 } Matrix pow(int k);//矩陣的k次冪,用快速冪實現,k為0時返回此矩陣的單位矩陣};Matrix operator*(const Matrix &m,const Matrix &n)//常量引用避免拷貝{ if(m.l_size()!=n.h_size())return Matrix();//非法運算返回空矩陣 Matrix ans(m.h_size(),n.l_size()); for(int i=0; i!=ans.h_size(); ++i) for(int j=0; j!=ans.l_size(); ++j) for(int k=0; k!=m.l_size(); ++k) ans[i][j]+=m[i][k]*n[k][j]; return ans;}Matrix Matrix::pow(int k){ if(k==0) { Matrix ans(h_size(),h_size()); for(int i=0; i!=ans.h_size(); ++i) ans[i][i]=1; return ans; } if(k==2)return (*this)*(*this); if(k%2)return pow(k-1)*(*this); return pow(k/2).pow(2);}
某公司有四個工廠,分佈在不同地區,同時三種產品,產量(單位;t),試用矩陣統計這些數據。
| 工廠\產品 | P1 | P2 | P3 |
|---|---|---|---|
| 甲 | 5 | 2 | 4 |
| 乙 | 3 | 8 | 2 |
| 丙 | 6 | 4 | |
| 丁 | 1 | 6 |
可用下述矩陣描述,其中四行分別表示甲乙丙丁四個工廠的生產情況,三列分佈表示三種產品P1,P2,P3的產量。
再設矩陣,其中第一列表示三種產品的單件利潤,第二列表示三種產品的單件體積。
矩陣C的第一列數據分別表示四個工廠的利潤,第二列分別表示四個工廠產品需要的存儲空間。
給定一個有向圖,問從A點恰好走k步(允許重複經過邊)到達B點的方案數。
把給定的圖轉為鄰接矩陣,即A(i,j)=1當且僅當存在一條邊i->j。令C=A*A,那麼C(i,j)=ΣA(i,k)*A(k,j),實際上就等於從點i到點j恰好經過2條邊的路徑數(枚舉k為中轉點)。類似地,C*A的第i行第j列就表示從i到j經過3條邊的路徑數。同理,如果要求經過k步的路徑數,我們只需要二分求出A^k即可。