層次分析法
運籌學理論
層次分析法,簡稱AHP,是指將與決策總是有關的元素分解成目標、準則、方案等層次,在此基礎之上進行定性和定量分析的決策方法。該方法是美國運籌學家匹茨堡大學教授薩蒂於20世紀70年代初,在為美國國防部研究"根據各個工業部門對國家福利的貢獻大小而進行電力分配"課題時,應用網路系統理論和多目標綜合評價方法,提出的一種層次權重決策分析方法。
層次分析法是指將一個複雜的多目標決策問題作為一個系統,將目標分解為多個目標或準則,進而分解為多指標(或準則、約束)的若干層次,通過定性指標模糊量化方法算出層次單排序(權數)和總排序,以作為目標(多指標)、多方案優化決策的系統方法。
層次分析法是將決策問題按總目標、各層子目標、評價準則直至具體的備投方案的順序分解為不同的層次結構,然後用求解判斷矩陣特徵向量的辦法,求得每一層次的各元素對上一層次某元素的優先權重,最後再加權和的方法遞階歸併各備擇方案對總目標的最終權重,此最終權重最大者即為最優方案。
層次分析法比較適合於具有分層交錯評價指標的目標系統,而且目標值又難於定量描述的決策問題。
層次分析法根據問題的性質和要達到的總目標,將問題分解為不同的組成因素,並按照因素間的相互關聯影響以及隸屬關係將因素按不同層次聚集組合,形成一個多層次的分析結構模型,從而最終使問題歸結為最低層(供決策的方案、措施等)相對於最高層(總目標)的相對重要權值的確定或相對優劣次序的排定。
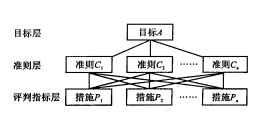
1.建立層次結構模型
將決策的目標、考慮的因素(決策準則)和決策對象按它們之間的相互關係分為最高層、中間層和最低層,繪出層次結構圖。最高層是指決策的目的、要解決的問題。最低層是指決策時的備選方案。中間層是指考慮的因素、決策的準則。對於相鄰的兩層,稱高層為目標層,低層為因素層。
2.構造判斷(成對比較)矩陣
在確定各層次各因素之間的權重時,如果只是定性的結果,則常常不容易被別人接受,因而Santy等人提出一致矩陣法,即不把所有因素放在一起比較,而是兩兩相互比較,對此時採用相對尺度,以儘可能減少性質不同的諸因素相互比較的困難,以提高準確度。如對某一準則,對其下的各方案進行兩兩對比,並按其重要性程度評定等級。為要素i與要素j重要性比較結果,表1列出Saaty給出的9個重要性等級及其賦值。按兩兩比較結果構成的矩陣稱作判斷矩陣。判斷矩陣具有如下性質:
判斷矩陣元素 的標度方法如下:
表1 比例標度表
| 因素i比因素j | 量化值 |
| 同等重要 | 1 |
| 稍微重要 | 3 |
| 較強重要 | 5 |
| 強烈重要 | 7 |
| 極端重要 | 9 |
| 兩相鄰判斷的中間值 | 2,4,6,8 |
3.層次單排序及其一致性檢驗
對應於判斷矩陣最大特徵根的特徵向量,經歸一化(使向量中各元素之和等於1)後記為W。W的元素為同一層次因素對於上一層次因素某因素相對重要性的排序權值,這一過程稱為層次單排序。能否確認層次單排序,則需要進行一致性檢驗,所謂一致性檢驗是指對A確定不一致的允許範圍。其中,n階一致陣的唯一非零特徵根為n;n 階正互反陣A的最大特徵根,當且僅當 時,A為一致矩陣。
由於λ連續的依賴於,則λ 比n 大的越多,A的不一致性越嚴重,一致性指標用CI計算,CI越小,說明一致性越大。用最大特徵值對應的特徵向量作為被比較因素對上層某因素影響程度的權向量,其不一致程度越大,引起的判斷誤差越大。因而可以用 λ-n 數值的大小來衡量A 的不一致程度。定義一致性指標為:
CI=0,有完全的一致性;CI 接近於0,有滿意的一致性;CI 越大,不一致越嚴重。
為衡量CI 的大小,引入隨機一致性指標 RI:
其中,隨機一致性指標RI和判斷矩陣的階數有關,一般情況下,矩陣階數越大,則出現一致性隨機偏離的可能性也越大,其對應關係如表2:
表2 平均隨機一致性指標RI標準值(不同的標準不同,RI的值也會有微小的差異)
| 矩陣階數 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| RI | 0.58 | 0.90 | 1.12 | 1.24 | 1.32 | 1.41 | 1.45 | 1.49 |
考慮到一致性的偏離可能是由於隨機原因造成的,因此在檢驗判斷矩陣是否具有滿意的一致性時,還需將CI和隨機一致性指標RI進行比較,得出檢驗係數CR,公式如下:
一般,如果CR<0.1 ,則認為該判斷矩陣通過一致性檢驗,否則就不具有滿意一致性。
4.層次總排序及其一致性檢驗
計算某一層次所有因素對於最高層(總目標)相對重要性的權值,稱為層次總排序。這一過程是從最高層次到最低層次依次進行的。
在運用層次分析法時,如果所選的要素不合理,其含義混淆不清,或要素間的關係不正確,都會降低AHP法的結果質量,甚至導致AHP法決策失敗。為保證遞階層次結構的合理性,需把握以下原則:
● ● 分解簡化問題時把握主要因素,不漏不多;
● ● 注意相比較元素之間的強度關係,相差太懸殊的要素不能在同一層次比較。
1.系統性的分析方法
層次分析法把研究對象作為一個系統,按照分解、比較判斷、綜合的思維方式進行決策,成為繼機理分析、統計分析之後發展起來的系統分析的重要工具。系統的思想在於不割斷各個因素對結果的影響,而層次分析法中每一層的權重設置最後都會直接或間接影響到結果,而且在每個層次中的每個因素對結果的影響程度都是量化的,非常清晰明確。這種方法尤其可用於對無結構特性的系統評價以及多目標、多準則、多時期等的系統評價。
2. 簡潔實用的決策方法
這種方法既不單純追求高深數學,又不片面地注重行為、邏輯、推理,而是把定性方法與定量方法有機地結合起來,使複雜的系統分解,能將人們的思維過程數學化、系統化,便於人們接受,且能把多目標、多準則又難以全部量化處理的決策問題化為多層次單目標問題,通過兩兩比較確定同一層次元素相對上一層次元素的數量關係后,最後進行簡單的數學運算。計算簡便,並且所得結果簡單明確,容易為決策者了解和掌握。
3. 所需定量數據信息較少
層次分析法主要是從評價者對評價問題的本質、要素的理解出發,比一般的定量方法更講求定性的分析和判斷。由於層次分析法是一種模擬人們決策過程的思維方式的一種方法,層次分析法把判斷各要素的相對重要性的步驟留給了大腦,只保留人腦對要素的印象,化為簡單的權重進行計算。這種思想能處理許多用傳統的最優化技術無法著手的實際問題。
1. 不能為決策提供新方案
層次分析法的作用是從備選方案中選擇較優者。在應用層次分析法的時候,可能就會有這樣一個情況,就是我們自身的創造能力不夠,造成了我們儘管在我們想出來的眾多方案里選了一個最好的出來,但其效果仍然不夠企業所做出來的效果好。而對於大部分決策者來說,如果一種分析工具能替我分析出在我已知的方案里的最優者,然後指出已知方案的不足,又或者甚至再提出改進方案的話,這種分析工具才是比較完美的。但顯然,層次分析法還沒能做到這點。
2. 定量數據較少,定性成分多,不易令人信服
在如今對科學的方法的評價中,一般都認為一門科學需要比較嚴格的數學論證和完善的定量方法。但現實世界的問題和人腦考慮問題的過程很多時候並不是能簡單地用數字來說明一切的。層次分析法是一種帶有模擬人腦的決策方式的方法,因此必然帶有較多的定性色彩。
3. 指標過多時,數據統計量大,且權重難以確定
當我們希望能解決較普遍的問題時,指標的選取數量很可能也就隨之增加。指標的增加就意味著我們要構造層次更深、數量更多、規模更龐大的判斷矩陣。那麼我們就需要對許多的指標進行兩兩比較的工作。由於一般情況下我們對層次分析法的兩兩比較是用1至9來說明其相對重要性,如果有越來越多的指標,我們對每兩個指標之間的重要程度的判斷可能就出現困難了,甚至會對層次單排序和總排序的一致性產生影響,使一致性檢驗不能通過。不能通過,就需要調整,在指標數量多的時候比較難調整過來。
4. 特徵值和特徵向量的精確求法比較複雜
在求判斷矩陣的特徵值和特徵向量時,所用的方法和我們多元統計所用的方法是一樣的。在二階、三階的時候,我們還比較容易處理,但隨著指標的增加,階數也隨之增加,在計算上也變得越來越困難。不過幸運的是這個缺點比較好解決,我們有三種比較常用的近似計算方法。第一種就是和法,第二種是冪法,還有一種常用方法是根法。
人們在對社會、經濟以及管理領域的問題進行系統分析時,面臨的經常是一個由相互關聯、相互制約的眾多因素構成的複雜系統。層次分析法則為研究這類複雜的系統,提供了一種新的、簡潔的、實用的決策方法。
層次分析法主要應用在安全科學和環境科學領域。在安全生產科學技術方面主要應用包括煤礦安全研究、危險化學品評價、油庫安全評價、城市災害應急能力研究以及交通安全評價等;在環境保護研究中的應用主要包括:水安全評價、水質指標和環境保護措施研究、生態環境質量評價指標體系研究以及水生野生動物保護區污染源確定等。除此之外,層次分析法更多的可以用於指導和解決個人生活中遇到的問題,比如說專業的選擇、工作的選擇以及買房的選擇等,可以通過建立層次結構以及衡量指標,來理清工作思路和思考問題的層面。