B-tree

B-tree

B-tree（多路搜索樹，並不是二叉的）是一種常見的數據結構。使用B-tree結構可以顯著減少定位記錄時所經歷的中間過程，從而加快存取速度。按照翻譯，B 通常認為是Balance的簡稱。這個數據結構一般用於資料庫的索引，綜合效率較高。

目錄
1節點內容 2性能特點 3用途用處
4平衡演算法 5其他樹含義

節點內容

B-tree中，每個結點包含：
1、本結點所含關鍵字的個數；
2、指向父結點的指針；
3、關鍵字；
4、指向子結點的指針；
對於一棵m階B-tree，每個結點至多可以擁有m個子結點。各結點的關鍵字和可以擁有的子結點數都有限制，規定m階B-tree中，根結點至少有2個子結點，除非根結點為葉子節點，相應的，根結點中關鍵字的個數為1~m-1；非根結點至少有[m/2]（[]，向上取整）個子結點，相應的，關鍵字個數為[m/2]-1~m-1。

性能特點

B-tree有以下特性：
1、關鍵字集合分佈在整棵樹中；
2、任何一個關鍵字出現且只出現在一個節點中；
3、搜索有可能在非葉子結點結束；
4、其搜索性能等價於在關鍵字全集內做一次二分查找；
5、自動層次控制；
由於限制了除根結點以外的非葉子結點，至少含有M/2個兒子，確保了結點的至少利用率，其最低搜索性能為：
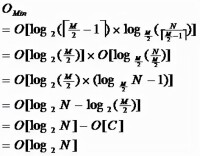
B-tree最低搜索性能
B-tree最低搜索性能
其中，M為設定的非葉子結點最多子樹個數，N為關鍵字總數；
所以B-樹的性能總是等價於二分查找（與M值無關），也就沒有B樹平衡的問題；
由於M/2的限制，在插入結點時，如果結點已滿，需要將結點分裂為兩個各佔M/2的結點；刪除結點時，需將兩個不足M/2的兄弟結點合併。

用途用處

鑒於B-tree具有良好的定位特性，其常被用於對檢索時間要求苛刻的場合，例如：
1、B-tree索引是資料庫中存取和查找文件(稱為記錄或鍵值)的一種方法。
2、硬碟中的結點也是B-tree結構的。與內存相比，硬碟必須花成倍的時間來存取一個數據元素，這是因為硬碟的機械部件讀寫數據的速度遠遠趕不上純電子媒體的內存。與一個結點兩個分支的二元樹相比，B-tree利用多個分支（稱為子數）的結點，減少獲取記錄時所經歷的結點數，從而達到節省存取時間的目的。

平衡演演算法

#define M 1
typedef int typekey;
typedef struct btnode {
int d;
typekey k[2*M];
char *v[2*M];
struct btnode *p[2*M+1];
} node, *btree;
extern int btree_disp;
extern char * InsValue;
extern btree search(typekey, btree);
extern btree insert(typekey,btree);
extern btree delete(typekey,btree);
extern int height(btree);
extern int count(btree);
extern double payload(btree);
extern btree deltree(btree);
#include
#include
#include "btrees.h"
btree search(typekey, btree);
btree insert(typekey,btree);
btree delete(typekey,btree);
int height(btree);
int count(btree);
double payload(btree);
btree deltree(btree);
static void InternalInsert(typekey, btree);
static void InsInNode(btree, int);
static void SplitNode(btree, int);
static btree NewRoot(btree);
static void InternalDelete(typekey, btree);
static void JoinNode(btree, int);
static void MoveLeftNode(btree t, int);
static void MoveRightNode(btree t, int);
static void DelFromNode(btree t, int);
static btree FreeRoot(btree);
static btree delall(btree);
static void Error(int,typekey);
int btree_disp;
char * InsValue = NULL;
static int flag;
static int btree_level = 0;
static int btree_count = 0;
static int node_sum = 0;
static int level;
static btree NewTree;
static typekey InsKey;
btree search(typekey key, btree t)
{
int i,j,m;
level=btree_level-1;
while (level >= 0)
{
if (key == t->k [ i ])
{
btree_disp = i;
return t;
}
if (key > t->k [ i ])
i++;
t = t->p[ i ];
level--;
}
return NULL;
}
btree insert(typekey key, btree t)
{
level=btree_level;
InternalInsert(key, t);
if (flag == 1)
t=NewRoot(t);
return t;
}
void InternalInsert(typekey key, btree t)
{
int i,j,m;
level--;
if (level < 0)
{
NewTree = NULL;
InsKey = key;
btree_count++;
flag = 1;
return;
}
if (key == t->k[ i ])
{
Error(1,key);
flag = 0;
return;
}
if (key > t->k[ i ])
i++;
InternalInsert(key, t->p[ i ]);
if (flag == 0)
return;
if (t->d < 2*M)
{
InsInNode(t, i);
flag = 0;
}
else
SplitNode(t, i);
}
void InsInNode(btree t, int d)
{
int i;
for(i = t->d; i > d; i--)
{
t->k[ i ] = t->k[i-1];
t->v[ i ] = t->v[i-1];
t->p[i+1] = t->p[ i ];
}
t->k[ i ] = InsKey;
t->p[i+1] = NewTree;
t->v[ i ] = InsValue;
t->d++;
}
void SplitNode(btree t, int d)
{
int i,j;
btree temp;
typekey temp_k;
char *temp_v;
temp = (btree)malloc(sizeof(node));
if (d > M)
{
for(i=2*M-1,j=M-1; i>=d; i--,j--)
{
temp->k[j] = t->k[ i ];
temp->v[j] = t->v[ i ];
temp->p[j+1] = t->p[i+1];
}
for(i=d-1,j=d-M-2; j>=0; i--,j--)
{
temp->k[j] = t->k[ i ];
temp->v[j] = t->v[ i ];
temp->p[j+1] = t->p[i+1];
}
temp->p[0] = t->p[M+1];
temp->k[d-M-1] = InsKey;
temp->p[d-M] = NewTree;
temp->v[d-M-1] = InsValue;
InsKey = t->k[M];
InsValue = t->v[M];
}
else
{
for(i=2*M-1,j=M-1; j>=0; i--,j--)
{
temp->k[j] = t->k[ i ];
temp->v[j] = t->v[ i ];
temp->p[j+1] = t->p[i+1];
}
if (d == M)
temp->p[0] = NewTree;
else
{
temp->p[0] = t->p[M];
temp_k = t->k[M-1];
temp_v = t->v[M-1];
for(i=M-1; i>d; i--)
{
t->k[ i ] = t->k[i-1];
t->v[ i ] = t->v[i-1];
t->p[i+1] = t->p[ i ];
}
t->k[d] = InsKey;
t->p[d+1] = NewTree;
t->v[d] = InsValue;
InsKey = temp_k;
InsValue = temp_v;
}
}
t->d =M;
temp->d = M;
NewTree = temp;
node_sum++;
}
btree delete(typekey key, btree t)
{
level=btree_level;
InternalDelete(key, t);
if (t->d == 0)
t=FreeRoot(t);
return t;
}
void InternalDelete(typekey key, btree t)
{
int i,j,m;
btree l,r;
int lvl;
level--;
if (level < 0)
{
Error(0,key);
flag = 0;
return;
}
for(i=0, j=t->d-1; i t->k[m])?(i=m+1):(j=m));
if (key == t->k[ i ])
{
if (t->v[ i ] != NULL)
free(t->v[ i ]);
if (level == 0)
{
DelFromNode(t,i);
btree_count--;
flag = 1;
return;
}
else
{
lvl = level-1;
r = t->p[ i ];
while (lvl > 0)
{
r = r->p[r->d];
lvl--;
}
t->k[ i ]=r->k[r->d-1];
t->v[ i ]=r->v[r->d-1];
r->v[r->d-1]=NULL;
key = r->k[r->d-1];
}
}
else if (key > t->k[ i ])
i++;
InternalDelete(key,t->p[ i ]);
if (flag == 0)
return;
if (t->p[ i ]->d < M)
{
if (i == t->d)
i--;
l = t->p [ i ];
r = t->p[i+1];
if (r->d > M)
MoveLeftNode(t,i);
else if(l->d > M)
MoveRightNode(t,i);
else
{
JoinNode(t,i);
return;
}
flag = 0;
}
}
void JoinNode(btree t, int d)
{
btree l,r;
int i,j;
l = t->p[d];
r = t->p[d+1];
l->k[l->d] = t->k[d];
l->v[l->d] = t->v[d];
for (j=r->d-1,i=l->d+r->d; j >= 0 ; j--,i--)
{
l->k[ i ] = r->k[j];
l->v[ i ] = r->v[j];
l->p[ i ] = r->p[j];
}
l->p[l->d+r->d+1] = r->p[r->d];
l->d += r->d+1;
free(r);
for (i=d; i < t->d-1; i++)
{
t->k[ i ] = t->k[i+1];
t->v[ i ] = t->v[i+1];
t->p[i+1] = t->p[i+2];
}
t->d--;
node_sum--;
}
void MoveLeftNode(btree t, int d)
{
btree l,r;
int m;
int i,j;
l = t->p[d];
r = t->p[d+1];
m = (r->d - l->d)/2;
l->k[l->d] = t->k[d];
l->v[l->d] = t->v[d];
for (j=m-2,i=l->d+m-1; j >= 0; j--,i--)
{
l->k[ i ] = r->k[j];
l->v[ i ] = r->v[j];
l->p[ i ] = r->p[j];
}
l->p[l->d+m] = r->p[m-1];
t->k[d] = r->k[m-1];
t->v[d] = r->v[m-1];
r->p[0] = r->p[m];
for (i=0; id-m; i++)
{
r->k[ i ] = r->k[i+m];
r->v[ i ] = r->v[i+m];
r->p[ i ] = r->p[i+m];
}
r->p[r->d-m] = r->p[r->d];
l->d+=m;
r->d-=m;
}
void MoveRightNode(btree t, int d)
{
btree l,r;
int m;
int i,j;
l = t->p[d];
r = t->p[d+1];
m = (l->d - r->d)/2;
r->p[r->d+m]=r->p[r->d];
for (i=r->d-1; i>=0; i--)
{
r->k[i+m] = r->k[ i ];
r->v[i+m] = r->v[ i ];
r->p[i+m] = r->p[ i ];
}
r->k[m-1] = t->k[d];
r->v[m-1] = t->v[d];
r->p[m-1] = l->p[l->d];
for (i=l->d-1,j=m-2; j>=0; j--,i--)
{
r->k[j] = l->k[ i ];
r->v[j] = l->v[ i ];
r->p[j] = l->p[ i ];
}
t->k[d] = l->k[ i ];
t->v[d] = l->v[ i ];
l->d-=m;
r->d+=m;
}
void DelFromNode(btree t, int d)
{
int i;
for(i=d; i < t->d-1; i++)
{
t->k[ i ] = t->k[i+1];
t->v[ i ] = t->v[i+1];
}
t->d--;
}
btree NewRoot(btree t)
{
btree temp;
temp = (btree)malloc(sizeof(node));
temp->d = 1;
temp->p[0] = t;
temp->p[1] = NewTree;
temp->k[0] = InsKey;
temp->v[0] = InsValue;
btree_level++;
node_sum++;
return(temp);
}
btree FreeRoot(btree t)
{
btree temp;
temp = t->p[0];
free(t);
btree_level--;
node_sum--;
return temp;
}
void Error(int f,typekey key)
{
if (f)
printf("Btrees error: Insert %d!\n",key);
else
printf("Btrees error: delete %d!\n",key);
}
int height(btree t)
{
return btree_level;
}
int count(btree t)
{
return btree_count;
}
double payload(btree t)
{
if (node_sum==0)
return 1;
return (double)btree_count/(node_sum*(2*M));
}
btree deltree (btree t)
{
level=btree_level;
btree_level = 0;
return delall(t);
}
btree delall(btree t)
{
int i;
level--;
if (level >= 0)
{
for (i=0; i < t->d; i++)
if (t->v[ i ] != NULL)
free(t->v[ i ]);
if (level > 0)
for (i=0; i<= t->d ; i++)
t->p[ i ]=delall(t->p[ i ]);
free(t);
}
return NULL;
}

其他樹含義

另外還有一種與此類似的樹結構叫B+樹，像 Berkerly DB , sqlite , mysql 資料庫都使用了B+樹演演算法處理索引。
B+和B-（即B）是因為每個結點上的關鍵字不同。一個多一個，一個少一個。
對於B+樹，其結點結構與B-tree相同，不同的是各結點的關鍵字和可以擁有的子結點數。如m階B+樹中，每個結點至多可以擁有m個子結點。非根結點至少有[m/2]個子結點，而關鍵字個數比B-tree多一個，為[m/2]~m。
這兩種處理索引的數據結構的不同之處：
1.B樹中同一鍵值不會出現多次，並且它有可能出現在葉結點，也有可能出現在非葉結點中。而B+樹的鍵一定會出現在葉結點中，並且有可能在非葉結點中也有可能重複出現，以維持B+樹的平衡。
2.因為B樹鍵位置不定，且在整個樹結構中只出現一次，雖然可以節省存儲空間，但使得在插入、刪除操作複雜度明顯增加。B+樹相比來說是一種較好的折中。
3.B樹的查詢效率與鍵在樹中的位置有關，最大時間複雜度與B+樹相同(在葉結點的時候)，最小時間複雜度為1(在根結點的時候)。而B+樹的時間複雜度對某建成的樹是固定的。

基本信息

中文名
多路搜索樹
外文名
B-tree
特點
綜合效率較高
屬性
數據結構