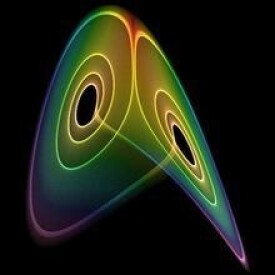
吸引子

那麼什麼是吸引子呢？吸引子是一個數學概念，描寫運動的收斂類型，它存在於相平面。簡言之，吸引子是指這樣的一個集合，當時間趨於無窮大時，在任何一個有界集上出發的非定常流的所有軌道都趨於它。這樣的集合有很複雜的幾何結構。由於吸引子與混沌現象密不可分，深入了解吸引子集合的性質，對更好了解它們所描述的流，對揭示出現混沌的規律與結構是很必要的。

從相空間上看，系統演化的目的體現為一定的點集合，代表演化過程的終極狀態，即目的態，具有如下特徵：

(1)終極性，處於非目的態的系統“不安於現狀”，力求離之遠去，處於目的態的系統則“安於現狀”，自身不再願意或無力改變這種狀態（也可以叫做惰性）。

(2)穩定性，目的態是系統自身質的規定性的體現，這種規定性只有在穩定狀態中才能確立起來並得到保持，不穩定狀態不可能成為目的態；

(3)吸引性，吸引性是目的性的根本要素，沒有吸引力的狀態不能成為系統演化所追求的目標。只要系統尚未到達目的態，現實狀態與目的態之間必定存在非0的吸引力，牽引著系統向目的態運動。相空間中滿足以上3個條件的點集合A(可能包含1個點、有限個點或無限個點)，被稱為動力學系統的吸引子。吸引子只能是定態，而且必須是穩定態。

其實，我們早已經接觸過吸引子了。在動力學里，就平面內的結構穩定系統——典型系統——而言，吸引子不外是：1.單個點2.穩定極限環。也可解釋為：長期運動不外是：1.靜止在定態2.周期性地重複某種運動系列。在非混沌體系中，這兩種情況都是“一般吸引子”，而在混沌體系中，第二種情況則被稱為：“奇怪吸引子”，它本身是相對穩定的，收斂的，但不是靜止的。奇怪吸引子是穩定的、具分形結構的吸引子。保守系統由於相體積永遠不變，所以不存在吸引子，而耗散系統則不然，相體積在演化過程中不斷收縮，各種各樣的運動在演化中逐漸衰亡，最後只剩下少數自由度決定的長時間行為，即：耗散系統的運動最終趨向維數比原始相空間低的極限集合，這個極限集合就是吸引子一個系統可能沒有吸引子，也可能同時存在多個吸引子。不同吸引子可能屬於同一類型，也可能屬於不同類型。原則上講，幾類吸引子的各種組合都可能出現。例如，同時存在幾個結點，或同時存在不動點和極限環，或同時存在不動點、極限環、奇怪吸引子，或同時有幾個奇怪吸引子，等等。

一般地，系統越複雜，吸引子(如果存在的話)結構就越複雜。那麼，如何刻畫或度量吸引子的複雜性，這是研究吸引子的重要內容。凡存在吸引子的系統，均為有目的的系統。從暫態向漸近穩定定態的運動過程，就是系統尋找目的的過程。所謂目的，就是在給定的環境中，系統只有在目的點或目的環上才是穩定的，離開了就不穩定，系統自己要拖到點或環上才能罷休。

一般來說，非線性系統可能具有0,1,2, ...等各種維數的平庸吸引子。高維吸引子最可能有準周期運動，而不是周期振動。然而自呂勒(Ruelle)和塔根斯(Takens)的工作以來，人們越來越清楚地看到，一般說來准周期軌道成為吸引子的可能性不大，更可能出現的是所謂奇怪吸引子。

奇怪吸引子是耗散系統混沌現象的另一個重要的特徵。簡單地說奇怪吸引子就是相空間（對連續的動力學系統，至少是三維；對離散的動力學系統，至少是二維）的一個有限的區域內，由無窮多個不穩定點集組成的一個集合體。奇怪吸引子有兩個最重要的特徵：（1）對初始條件有敏感的依賴性。在初始時刻從這個奇怪吸引子上任何兩個非常接近的點出發的兩條運動軌道，最終必會以指數的形式互相分離。由於混沌對初值極為敏感，它表現為局部不穩定。但對耗散系統而言，則又具有相體積收縮的特性，因而造成軌道無窮多次折迭往返。混沌軌道在相空間中"添滿"有限的區域，形成奇怪吸引子。實際上，它有內外兩種趨向，一切吸引子之外的運動都向它靠攏，這是穩定的方向；而一

切到達吸引子內的軌道都又相互排斥（指數式分離），對應為不穩定方向。正是這種整體趨向穩定而局部又極為不穩定的矛盾，導致了奇怪吸引子的另一個更奇怪的性質： （2）它具有非常奇特的拓撲結構和幾何形式。奇怪吸引子是具有無窮多層次自相似結構的、幾何維數為非整數的一個集合體。為了描述奇怪吸引子的這種奇特結構，andelbrot率先引進了分形（既其維數是非整數的對象）的概念。

作為相空間點集合的吸引子，其維數必定低於空間的維數。低維性是吸引子的重要特徵之一，因為系統尋找目的態的過程必定是降維的過程。

當相空間同時存在幾個吸引子時，整個相空間將以它們為中心劃分為幾個區域，每個區域內的軌道都以該吸引子為歸宿，稱為該吸引子的吸引域或流域。吸引子理論認為，複雜系統在狀態空間中的行為軌線是由動力方程來表示的。它的動力學方程一般地是由一組“吸引子”所決定的。系統向哪個吸引子演化，取決於初態落在那個吸引域里，系統最終達到哪個吸引子是不確定的，一些微小的漲落都會導致系統走向某個吸引子而不走向另一個吸引子。

吸引子是刻劃系統整體特性的概念，具有 不可分割性，即不能把它劃分為兩個都滿足定義要求的較小集合。也不能把幾個吸引子組合為一個吸引子，如平衡態A與周期態B不能合成一個單一的吸引子。

在動態系統理論中，排斥子又稱為源，吸引子又稱為匯。一切有實際意義的軌道總是從源流向匯

。處於不穩定定態的系統也“安於現狀”，自身沒有改變現狀的動力。但它們對附近的軌道沒有吸

引力，反而有排斥力。一旦擾動使系統離開這種定態，排斥力將使任何軌道遠離該定態而去。由此緣

故，不穩定的結點、焦點、極限環、環面被稱為排斥子。研究排斥子也是吸引子理論的重要內容。