公共弦
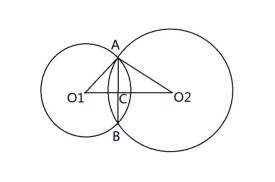
公共弦
當兩個圓相交時,兩個交點的連線叫公共弦。(若只有一個交點,則稱公共點。)兩圓心所在直線垂直平分公共弦。
公共弦
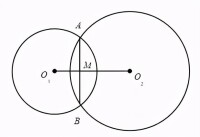
兩個圓若是相交,則至多交於2點。而將兩圓的方程相減即是默認兩條方程中有共同的解X、Y。而減后的方程必定滿足X、Y(就是兩個交點),換句話說,就是兩個交點所共同滿足的直線方程。而我們知道,平面內2點間有且只有1條直線,那麼這條直線就是所求的公共弦。
若圓C1:(x-a1)^2+(y-b1)^2=r1^2或x2+y2+D1x+E1y+F1=0
圓C2:(x-a2)^2+(y-b2)^2=r2^2或x2+y2+D2x+E2y+F2=0
則過兩圓交點的直線方程為:(x-a1)^2+(y-b1)^2-(x-a2)^2-(y-b2)^2=r1^2-r2^2 或 (D1-D2)x+(E1-E2)y+F1-F2=0
這是“兩相交圓方程相減得公共弦方程”的變式
設兩圓分別為
x^2+y^2+c1x+d1y+e1=0 ①
x^2+y^2+c2x+d2y+e2=0 ②
兩式相減得
(x^2+y^2+c1x+d1y+e1)-(x^2+y^2+c2x+d2y+e2)=0 ③
這是一條直線的方程
(1)先證這條直線過兩圓交點
設交點為(x0,y0)則滿足①②
所以滿足③
所以交點在直線③上
(2)由於過兩交點的直線又且只有一條
所以得證