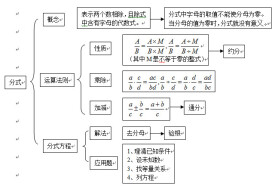
分式

形如（A、B是整式，B中含有字母）的式子叫做分式。其中A叫做分式的分子，B叫做分式的分母。

當分式的分子的次數低於分母的次數時，我們把這個分式叫做真分式；當分式的分子的次數高於分母的次數時，我們把這個分式叫做假分式。

注意：判斷一個式子是否是分式，不要看式子是否是的形式，關鍵要滿足：分式的分母中必須含有字母，分子分母均為整式。無需考慮該分式是否有意義，即分母是否為零。

由於字母可以表示不同的數，所以分式比分數更具有一般性。

方法：數看結果，式看形。

1.分式有意義條件：分母不為0。

2.分式值為0條件：分子為0且分母不為0。

3.分式值為正(負)數條件：分子分母同號得正，異號得負。

4.分式值為1的條件：分子=分母≠0。

5.分式值為-1的條件：分子分母互為相反數，且都不為0。

整式和分式統稱為有理式。

帶有根號且根號下含有字母的式子叫做無理式。

無理式和有理式統稱代數式。

分式的分子和分母同時乘以（或除以）同一個不為0的整式，分式的值不變。用式子表示為：

其中A,B,C為整式，且B、C≠0。

根據分式基本性質，可以把一個分式的分子和分母的公因式約去，這種變形稱為分式的約分。約分的關鍵是確定分式中分子與分母的公因式。

步驟：

1.如果分式的分子和分母都是單項式或者是幾個因式乘積的形式，將它們的公因式約去。

2.分式的分子和分母都是多項式，將分子和分母分別分解因式，再將公因式約去。

係數取分子和分母係數的最大公約數，字母取分子和分母共有的字母，指數取公共字母的最小指數，即為它們的公因式。

一個分式不能約分時，這個分式稱為最簡分式。約分時，一般將一個分式化為最簡分式。乘法同分母分式的加減法法則進行計算。用字母表示為：兩個分式相乘，把分子相乘的積作為積的分子，把分母相乘的積作為積的分母。用字母表示為：

。

兩個分式相除，把除式的分子和分母顛倒位置后再與被除式相乘：。

也可表述為：除以一個分式，等於乘以這個分式的倒數。

分子乘方做分子，分母乘方做分母，可以約分的約分，最後化成最簡：。