共找到2條詞條名為queue的結果 展開
- 線性表
- 英文單詞
queue
線性表
隊列是一種特殊的線性表,是一種先進先出(FIFO)的數據結構。它只允許在表的前端(front)進行刪除操作,而在表的後端(rear)進行插入操作。進行插入操作的端稱為隊尾,進行刪除操作的端稱為隊頭。隊列中沒有元素時,稱為空隊列。
在隊列這種數據結構中,最先插入在元素將是最先被刪除;反之最後插入的元素將最後被刪除,因此隊列又稱為“先進先出”(FIFO—first in first out)的線性表。
隊列空的條件:front=rear
隊列滿的條件: rear = MAXSIZE
隊列可以用數組Q[1…m]來存儲,數組的上界m即是隊列所容許的最大容量。在隊列的運算中需設兩個指針:head,隊頭指針,指向實際隊頭元素的前一個位置;tail,隊尾指針,指向實際隊尾元素所在的位置。一般情況下,兩個指針的初值設為0,這時隊列為空,沒有元素。圖1 ( a)畫出了一個由6個元素構成的隊列,數組定義Q[1…10]。Q(i) i=3,4,5,6,7,8頭指針head=2,尾指針tail=8。隊列中擁有的元素個數為:L=tail-head現要讓排頭的元素出隊,則需將頭指針加1。即head=head+1這時頭指針向上移動一個位置,指向Q(3),表示Q(3)已出隊。見圖1 (b)。如果想讓一個新元素入隊,則需尾指針向上移動一個位置。即tail=tail+1這時Q(9)入隊。當隊尾已經處理在最上面時,即tail=10,如果還要執行入隊操作,則要發生"上溢",但實際上隊列中還有三個空位置,所以這種溢出稱為"假溢出"。
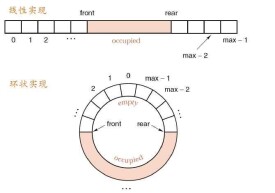
克服假溢出的方法有兩種。一種是將隊列中的所有元素均向低地址區移動,顯然這種方法是很浪費時間的;另一種方法是將數組存儲區看成是一個首尾相接的環形區域。當存放到n地址后,下一個地址就"翻轉"為1。在結構上採用這種技巧來存儲的隊列稱為循環隊列。
隊列和棧一樣只允許在端點(前端或者後端)處插入和刪除元素。
循環隊的入隊演演算法如下:
1、tail=tail+1;
2、若tail=n+1,則tail=1;
3、若head=tail尾指針與頭指針重合了,表示元素已裝滿隊列,則作上溢出錯處理;
4、否則,Q(tail)=X,結束(X為新入出元素)。
隊列和棧一樣,有著非常廣泛的應用。
(1)初始化隊列 Qini (Q)
(2)入隊 QADD(Q,X)
(3)出隊 QDel(Q,X)
(4)判斷隊列是否為空 qempty(Q)
(5)判斷隊列是否為滿qfull(Q)
queue類是為程序員提供了一個隊列的功能的容器適配器,具體而言,一個FIFO(先入先出)的數據結構
在頭文件中定義(在程序開頭輸入#include ,切記不可寫為#include )。
原型
| q.empty() | 判斷隊列q是否為空,當隊列q空時,返回true;否則為false(值為0(false)/1(true))。 |
| q.size() | 訪問隊列q中的元素個數。不可寫成sizeof(q)或size(q) |
| q.push() | 會將一個元素a置入隊列q中 |
| q.front() | 返回隊列q內的第一個元素(也就是第一個被置入的元素)。(不可寫成front(q)) |
| q.back() | 會返回隊列q中最後一個元素(也就是最後被插入的元素)。(不可寫成back(q)) |
| q.pop() | 會從隊列q中移除第一個元素。(不可寫成pop(q)) |
• 注意:pop()雖然會移除下一個元素,但是並不返回它。
• front()和back()返回下一個元素但並不移除該元素。
• 在stack庫中的函數與queue很類似,但是stack中要返回元素時,只能返回最後一個元素,且函數名不一樣(stack中為s.top()),需要區分。 [1]