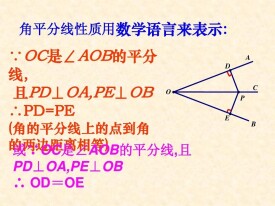
角平分線的性質
角的平分線上的點到角的兩邊的距離相等
三角形的一個內角的平分線與它的對邊相交,連接這個角的頂點和交點之間的線段叫三角形的角平分線。(也叫三角形的內角平分線。)角平分線的性質,主要有1,角的平分線上的點到角的兩邊的距離相等,是指點到直線的距離,在應用時必須含有垂直這個條件 否則不能得到線段相等,外角平分線上的點到角兩邊的反向延長線的距離相等,角的平分線上的點到角的兩邊的距離相等;2,角平分線分得的兩個角相等,都等於該角的一半;3,三角形的三條角平分線交於一點,稱作三角形內心。三角形的內心到三角形三邊的距離相等。
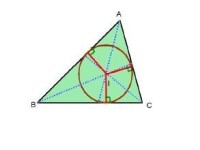
角平分線的性質
定理
角平分線
性質1:在角平分線上的點到這個角的兩邊的距離相等。性質2:到一個角的兩邊的距離相等的點,在這個角的平分線上。綜合性質1與性質2,可得到如下結論:角的平分線是到角的兩邊距離相等的所有點的集合。三角形內角平分段性質定理,其內容是:三角形內角平分線分對邊所成的兩條線段,和兩條鄰邊成比例。
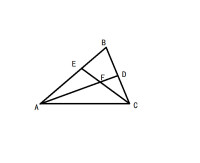
●三角形內角平分線分對邊所成的兩條線段,和兩條鄰邊成比例.
即 在三角形ABC中,當AD是頂角A的角平分線交底邊於D時,BD/CD=AB/AC.
證明:
如圖,AD為△ABC的角平分線,過點D向邊AB,AC分別引垂線DE,DF.則DE=DF.
S△ABD:S△ACD=BD/CD
又因為S△ABD:S△ACD=[(1/2)AB×DE]:[(1/2)AC×DF]=AB:AC
所以BD/CD=AB/AC.
角
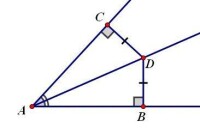
第二部分2.角平分線線上的點到角兩邊的距離相等。如右上圖,若射線AD是∠CAB的角平分線,求證:CD=BD∵∠DCA=∠DBA∠CAD=∠BADAD=AD∴△ACD≌△ABD∴CD=BD
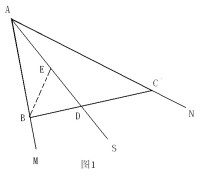
圖1
第四部分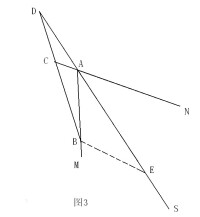 4.三角形一個角的平分線,這個角平分線其對邊所成的兩條線段與這個角的兩鄰邊對應成比例。如右下圖,平面內任意一小於180度的∠MAN,AS平分∠MAN,直線BC分別交射線AM、AN、AS於B、C、D,求證:AB/BD=AC/CD:作BE=BD交射線AS於E,如圖1:∵BE=BD,∴∠BED=∠BDE,∴∠AEB=∠ADC又∵∠BAE=∠CAD,∴△AEB∽△ADC,∴AB/BE=AC/CD, 即AB/BD=AC/CD.另外的情況,如圖2,直線BC交AS的反向延長線於D,如圖3,直線BC交AN的反向延長線於C;此時,仍有AB/BD=AC/CD證法與圖1類似逆定理
4.三角形一個角的平分線,這個角平分線其對邊所成的兩條線段與這個角的兩鄰邊對應成比例。如右下圖,平面內任意一小於180度的∠MAN,AS平分∠MAN,直線BC分別交射線AM、AN、AS於B、C、D,求證:AB/BD=AC/CD:作BE=BD交射線AS於E,如圖1:∵BE=BD,∴∠BED=∠BDE,∴∠AEB=∠ADC又∵∠BAE=∠CAD,∴△AEB∽△ADC,∴AB/BE=AC/CD, 即AB/BD=AC/CD.另外的情況,如圖2,直線BC交AS的反向延長線於D,如圖3,直線BC交AN的反向延長線於C;此時,仍有AB/BD=AC/CD證法與圖1類似逆定理 【角平分線逆定理】1.到角兩邊的距離相等的點在角平分線上。2.平面內任意一小於180度的∠MAN如圖,直線BC分別交半直線AM、AN、AS於B、C、D,AB/BD=AC/CD則:AS平分∠MAN下面給出證明過程:證明:過B作BH∥AC交AS於H∴△ADC∽△HDB(∠ADC=∠HDB,∠ACD=∠HBD)∴AC/CD=HB/BD又AB/BD=AC/CD∴AB=BH∴∠BHA=∠BAH=∠HAC∴AS平分∠MAN
【角平分線逆定理】1.到角兩邊的距離相等的點在角平分線上。2.平面內任意一小於180度的∠MAN如圖,直線BC分別交半直線AM、AN、AS於B、C、D,AB/BD=AC/CD則:AS平分∠MAN下面給出證明過程:證明:過B作BH∥AC交AS於H∴△ADC∽△HDB(∠ADC=∠HDB,∠ACD=∠HBD)∴AC/CD=HB/BD又AB/BD=AC/CD∴AB=BH∴∠BHA=∠BAH=∠HAC∴AS平分∠MAN

圖3

角