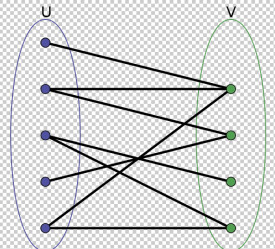
二分圖

二分圖又稱作二部圖、兩偶圖，是圖論中的一種特殊模型。設是一個無向圖，如果頂點V可分割為兩個互不相交的子集，並且圖中的每條邊所關聯的兩個頂點i和j分別屬於這兩個不同的頂點集，則稱圖G為一個二分圖。

簡而言之，就是頂點集V可分割為兩個互不相交的子集，並且圖中每條邊依附的兩個頂點都分屬於這兩個互不相交的子集。

區別二分圖，關鍵是看點集是否能分成兩個獨立的點集。

圖1中U和V構造的點集所形成的循環圈不為奇數，所以是二分圖。

圖2中U和V和W構造的點集所形成的的循環圈為奇數，所以不是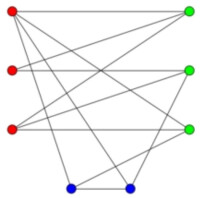二分圖。

無向圖G為二分圖的充分必要條件是，G至少有兩個頂點，且其所有迴路的長度均為偶數。

證先證必要性。

設G為二分圖。由於X，Y非空，故G至少有兩個頂點。若C為G中任一迴路，令

其中諸必定相間出現於X及Y中，不妨設

因此l必為偶數，從而C中有偶數條邊。

再證充分性。

設G的所有迴路具有偶數長度，並設G為連通圖（不失一般性，若G不連通，則可對G的各連通分支作下述討論）。

令G的頂點集為V，邊集為E，現構作X，Y，使 。取，置

X顯然非空。現需證Y非空，且沒有任何邊的兩個端點都在X中或都在Y中。

由於並且G為一連通圖，因此v0必定有相鄰頂點，設為v1，那麼；故Y不空。

設有邊，使。那麼，v0到u有偶數長度的通路，或；v0到v有偶數長度的通路，或。無論何種情況，均有一條從v0到v0的奇數長度的閉路徑，因而有從v0到v0的奇數長度的迴路（因從閉路徑上可能刪去的迴路長度總為偶數），與題設矛盾。故不可能有邊使u,v均在X中。

“沒有任何邊的兩個端點全在Y中”的證明可仿上進行，請讀者思考。

給定一個二分圖G，在G的一個子圖M中，M的邊集中的任意兩條邊都不依附於同一個頂點，則稱M是一個匹配.

選擇這樣的邊數最大的子集稱為圖的最大匹配問題（maximal matching problem)

如果一個匹配中，圖中的每個頂點都和圖中某條邊相關聯，則稱此匹配為完全匹配，也稱作完備匹配.

求最大匹配的一種顯而易見的演演算法是：先找出全部匹配，然後保留匹配數最多的。但是這個演演算法的複雜度為邊數的指數級函數。因此，需要尋求一種更加高效的演演算法.

增廣路的定義（也稱增廣軌或交錯軌）：

若P是圖G中一條連通兩個未匹配頂點的路徑，並且屬M的邊和不屬M的邊（即已匹配和待匹配的邊）在P上交替出現，則稱P為相對於M的一條增廣路徑.

由增廣路的定義可以推出下述三個結論：

1-P的路徑長度必定為奇數，第一條邊和最後一條邊都不屬於M.

2-P經過取反操作可以得到一個更大的匹配M'.

3-M為G的最大匹配當且僅當不存在相對於M的增廣路徑.

匈牙利演演算法

用增廣路求最大匹配（稱作 匈牙利演演算法，匈牙利數學家Edmonds於1965年提出）

演演算法輪廓：

⑴置M為空

⑵找出一條增廣路徑P，通過取反操作獲得更大的匹配M'代替M

⑶重複⑵操作直到找不出增廣路徑為止

g:array[1..maxn,1..maxm]of boolean;

y:array[1..maxm]of boolean;

link:array[1..maxm]of longint;

function find(v:longint):boolean;

var i:longint;

begin

for i:=1 to m do

if g[v,i] and (not y[ i ]) then

begin

y[ i ]:=true;

if (link[ i ]=0)or find(link[ i ]) then

begin

link[ i ]:=v;

find:=true;

exit;

end;

end;

find:=false;

end;

begin

//read the graph into array g[][]

for i:=1 to n do

begin

fillchar(y,sizeof(y),0);

if find(i) then inc(ans);

end;

其中n,m分別為2部圖兩邊節點的個數，兩邊的節點分別用1..n,1..m編號

表示x,y兩個點之間有邊相連

記錄的是當前與y節點相連的x節點

y記錄的是y中的i節點是否被訪問過.

演演算法的思路是不停的找增廣軌，並增加匹配的個數，增廣軌顧名思義是指一條可以使匹配數變多的路徑，在匹配問題中，增廣軌的表現形式是一條"交錯軌",也就是說這條由圖的邊組成的路徑，它的第一條邊是目前還沒有參與匹配的，第二條邊參與了匹配，第三條邊沒有..最後一條邊沒有參與匹配，並且始點和終點還沒有被選擇過。這樣交錯進行，顯然他有奇數條邊。那麼對於這樣一條路徑，我們可以將第一條邊改為已匹配，第二條邊改為未匹配...以此類推。也就是將所有的邊進行" 反色",容易發現這樣修改以後，匹配仍然是合法的，但是匹配數增加了一對。另外，單獨的一條連接兩個未匹配點的邊顯然也是交錯軌。可以證明，當不能再找到增廣軌時，就得到了一個最大匹配。這也就是匈牙利演演算法的思路.

代碼中find(i）就是尋找有沒有從x點i開始的增廣軌，如果有就進行上述操作，代碼是遞歸的，所以看起來不是很顯然，畫個圖試試就很清楚了.

//其中n,m分別為2部圖兩邊節點的個數，兩邊的節點分別用1..n,1..m編號

bool g[n][m];//g[x][y]表示x,y兩個點之間有邊相連

bool y[m];//y[i]記錄的是y中的i節點是否被訪問過.

int link[m];//link[y]記錄的是當前與y節點相連的x節點

bool find(int v)

{

int i;

for(i=0;i

{

if(g[v][i]&&!y[i])

{

y[i]=true;

if(link[i]==0||find(link[i])

{

link[i]=v;

return true;

}

}

}

return false;

}

int main()

{

//read the graph int array g[][]

for(i=0;i

{

memset(y,0,sizeof(y));

if(find(i)) ans++;

}

return 0;

}