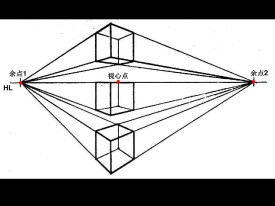
成角透視
成角透視
成角透視就是景物縱深與視中線成一定角度的透視，景物的縱深因為與視中線不平行而向主點兩側的余點消失。成角透視多用於室外繪畫，可以表現2個畫面。
成角透視:(兩點透視）就是把立方體畫到畫面上，立方體的四個面相對於畫面傾斜成一定角度時，往縱深平行的直線產生了兩個消失點。在這平行情況下，與上下兩個水平面相垂直的平行線也產生了長度的縮小，但是不帶有消失點.平行透視是景物縱深與視中線平行而向主點消失。成角透視就是景物縱深與視中線成一定角度的透視，景物的縱深因為與視中線不平行而向主點兩側的余點消失。
成角透視就是景物縱深與視中線成一定角度的透視，凡是與畫面既不平行又不垂直的水平直線，都消失於視平線上的一點，叫消失點，余點在視平線上，景物的縱深因為與視中線不平行而向主點兩側的余點消失。凡是平行的直線都消失於同一個余點，例如樓房的每層分界線都消失於同一個余點。所以，對於立方體景物，在成角透視中都有兩個余點，這兩個余點在主點兩側，如右圖。
成角透視：(二點透視）就是把立方體畫到畫面上，立方體的四個面相對於畫面傾斜成一定角度時，往縱深平行的直線產生了兩個消失點。在這平行情況下，與上下兩個水平面相垂直的平行線也產生了長度的縮小，但是不帶有消失點，平行透視是景物縱深與視中線平行而向主點消失。成角透視就是景物縱深與視中線成一定角度的透視，景物的縱深因為與視中線不平行而向主點兩側的余點消失。
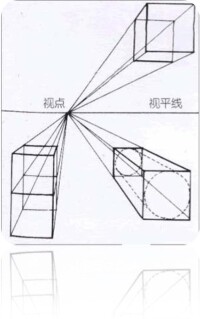
成角透視
兩點透視又稱為成角透視，由於在透視的結構中，有兩個透視消失點(滅點)，因而得名。
物體有一組垂直線與畫面平行，其他兩組線均與畫面成一定角度，而每組有一個消失點，共有兩個消失點(也叫余點，它分佈在心點的兩側的視平線上，分為左余點和右余點)，稱為二點透視，也稱為成角透視。二點透視圖畫面效果比較自由、活潑，能比較真實地反映空間，可以反映建築物的正側兩面，容易表現出體積感。另外，有較強的明暗對比效果，變化比較豐富，是建築設計中一種常見的表現手法。
成角透視又稱二點透視，就是把立方體畫到畫面上，立方體的四個面相對於畫面傾斜成一定角度時，往縱深平行的直線產生了兩個消失點。在這種平行情況下。與上下兩個水平面相垂直的平行線也產生了長度的縮小，但是不帶有消失點。平行透視是景物縱深與視中線平行而向主點消失。成角透視就是景物縱深與視中線成一定角度的透視，景物的縱深因為與視中線不平行而向主點兩側的余點消失。
根據60度視域的一些限制，一般成角透視的兩側余點不能同時出現在畫面裡面。通過延長線虛擬定位的兩個余點之間的距離一般最理想長度以畫面對角線的1.5倍為宜。在繪圖時，要特別注意的是兩個余點必然在畫面的視平線上。
1．成角透視所畫的空間和物體，都是與畫面有一定偏角的立方體，視向為平視，有左右兩個方向的消失點。
2．一條邊貼近於畫面。
3．方形物體的透視現象是隨著物體的位置變化和人的視角變化而千變萬化的，從一件立方體旋轉與畫面成角大小的變化可以認識立方體的透視變化特點和一對消失點沿著視平線(地平線)移動的規律。
4．三組平行線三個方向，直立的平行線是原線，互相平行沒有消失點。
基本信息
- 中文名
- 成角透視
- 外文名
- Angular Perspective
- 別名
- 二點透視
- 定義
- 景物縱深與視中線成一定角度
- 特點
- 有兩個透視消失點
- 應用領域
- 建築設計