帶狀矩陣
帶狀矩陣
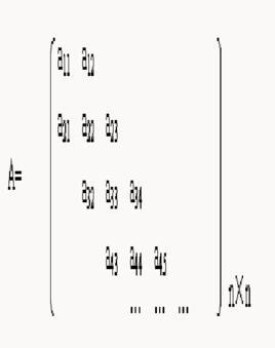
帶狀矩陣即在矩陣A中,所有的非零元素都集中在以主對角線為中心的帶狀區域中。
對於n*n的方陣,若它的全部非零元素落在一個以主對角線為中心的帶狀區域中,這個帶狀區域包含主對角線,以及主對角線下面及上面各b條對角線上的元素,那麼稱該方陣為半帶寬為b的帶狀矩陣。
帶狀矩陣的特點是:對於矩陣元素a(i,j)!=0,|i-j|<=b。
帶狀矩陣的存儲空間為(2*b+1)*n-2*b。2*b+1為每一行所需空間,所以乘以n行,又因為第一行和最後一行之分配b+1個空間,所以公式中要減去2倍的2*b+1-(b+1)=b。
address(a(i,j))=1+(i*(2*b+1)-b)+(j-i+b)=1+(i*(2*b+1)+j-i)。我把書中的公式做了修改,address(a(i,j))=1。紅色字體表示元素所在行之前的元素個數。每一行有2*b+1個元素,之前有i行,由於第一行並沒有2*b+1個元素,所以要減去b個。
n階矩陣A稱為帶狀矩陣,如果存在最小正數m ,滿足當∣i-j∣ ≥ m 時,aij =0,這時稱 w=2m-1 為矩陣A的帶寬;
亦可表述為:對於n階對稱矩陣A,若存在最小正數m,使j > i+m時,aij =0,這時稱 w=2m+1 為矩陣A的帶寬。
帶狀矩陣指矩陣中所有的非零元素都集中在以對角線為中心的帶狀區域中,這裡以最常見的三對角帶狀矩陣為例,示例代碼: