周長
環繞有限面積邊緣的長度積分
環繞有限面積的區域邊緣的長度積分,叫做周長,也就是圖形一周的長度。多邊形的周長的長度也相等於圖形所有邊的和,圓的周長=πd=2πr (d為直徑,r為半徑,π),扇形的周長 = 2R+nπR÷180˚ (n=圓心角角度) = 2R+kR (k=弧度)。
環繞限積區域緣積,周,圖形周。周示。
圓:(d為直徑,r為半徑,π)
角形周(abc為三角形的三條邊)
四邊形:(abcd為四邊形的邊長)
周長
正方形:(a為正方形的邊長)
多邊形:。
扇形的周長:
如果以同一面積的三角形而言,以等邊三角形的周界最短;如果以同一面積的四邊形而言,以正方形的周界是最短;如果以同一面積的五邊形而言,以正五邊形的周界最短;如果以同一面積的任意多邊形而言,以正圓形的周界最短。周長只能用於二維圖形(平面、曲面)上,三維圖形(立體)如柱體、錐體、球體等都不能以周界表示其邊界大小,而是要用總表面面積。
。
“周長的認識”是義務教育數學第一學段三年級(上冊)的學習內容,課程標準關於“周長的認識”的學習內容,實際上包含三個層面:首先是讓學生認識到周長的概念,並能在實際生活中體驗周長;其次是讓學生掌握測量周長的方法和過程;最後是體驗和感受數學在生活中的應用。
課程標準對於“周長的認識”這一具體的課程內容,在內容標準中明確指出了目標要求,即“指出並測量具體圖形的周長,探索並掌握長方形、正方形的周長公式”。此外,在數學課程的總體目標中,“獲得一些初步的數學實踐活動經驗,能夠運用所學的知識和方法解決簡單的問題;感受數學在日常生活中的作用”,也是對於“周長的認識”的目標要求。
這裡的課程目標,其實是知識與技能、數學思考、解決問題、情感與態度目標的細化和具體體現,這些目標要求涉及第一學段“學段目標”的如下要求:知識與技能目標中的“獲得初步的測量(包括估測)的技能”;數學思考目標中的“在對簡單物體和圖形的形狀、大小、位置關係、運動的探索過程中,發展空間觀念”;解決問題目標中的“了解同一問題可以有不同的解決辦法。有與同伴合作解決問題的體驗。初步學會表達解決問題的大致過程和結果”;以及情感與態度目標中的“在他人的鼓勵與幫助下,對身邊與數學有關係的某些事物有好奇心,能夠積極參與生動、直觀的數學活動。感受數學與日常生活的密切聯繫。經歷觀察、操作、歸納等數學思考過程的合理性。在他人的指導下能夠發現數學活動中的錯誤並及時改正”。
隨著社會的發展,各式各樣的儀器孕育而生,目的都是為了滿足人們實際生活和工作的需要。周長和面積測量儀也不例外,它的目的同樣是幫助人們方便、快捷、準確地測量任意平面圖形的周長和面積。
一種周長和面積測量儀的原理主要是利用了變換器原理,將一條曲線按照任意給定的規律轉換成另一條曲線。該機構應有兩個自由度,以使一點被迫沿導引線運動時,各構件上一些確定的點描繪出完全確定的軌跡。該測量儀器將連桿、滑塊、滾輪三者巧妙地結合起來,具有結構簡單、測量精準度高、使用方便等特點。
測量儀器結構分析
如圖1所示,d為平面內任意圖形。整個機構由連桿、滑塊、滾輪組成。在連桿 的長度段上,設 和 是滑塊,且只能在導引直線軌道內滑動。C是一半徑為r的滾輪,且保證在測量過程中作純滾動。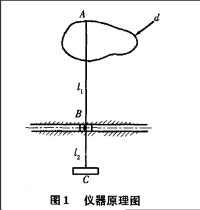

周長
機構運動學分析:只有在自由度大於等於2的情況下,才能保證滾輪C作純滾動。很容易計算出該機構的自由度。
周長測量儀原理分析
當A點沿著被測圖形的輪廓繞行時,滑塊B被迫沿著導引直線軌跡運動,滾輪也跟著做純滾動。這樣就可以利用滾輪轉動的角度來計算出曲線的長度。
如圖2所示,假設A點運動到A’點,B點運動到點B',這時,C點運動到C'點。設A點移動了ds距離,B點移動了dl距離。滾輪滾動的角度如圖3所示。設滾輪滾過角度為da。滾輪無論順時針旋轉還是逆時針旋轉,角度計數器都記錄正值。
再將直線AC複製到B‘點處,得到直線。設A'C'與偏移的角度為。
微線段AA’的長度:
B點移動的距離:
由上述兩式聯立,
對式(3)進行積分就可得到曲線的長度s。
