隨機抽樣
隨機抽樣
按照隨機的原則,即保證總體中每一個對象都有已知的、非零的概率被選入作為研究的對象,保證樣本的代表性。隨機抽樣法就是調查對象總體中每個部分都有同等被抽中的可能,是一種完全依照機會均等的原則進行的抽樣調查,被稱為是一種“等概率”。隨機抽樣有四種基本形式,即簡單隨機抽樣、等距抽樣、類型抽樣和整群抽樣。
它的最大優點是在根據樣本資料推論總體時,可用概率的方式客觀地測量推論值的可靠程度,從而使這種推論建立在科學的基礎上。正因為此,隨機抽樣在社會調查和社會研究中應用較廣泛。常用的隨機抽樣方法主要有純隨機抽樣、分層抽樣、系統抽樣、整群抽樣、多階段抽樣等。
隨機抽樣是在全部調查單位中按照隨機原則抽取一部分單位進行調查,根據調查結果推斷總體的一種調查方式。
隨機抽樣具有以下幾個基本特點。
(1)按照隨機原則抽選調查單位。所謂隨機原則就是指樣本單位的抽取不受任何主觀因素及其他系統性因素的影響,總體的每個單位都有一定的機會被抽選為樣本單位。
(2)對部分單位調查的目的是為了推斷總體指標。根據數理統計原理,抽樣調查中的樣本指標和對應的總體指標之間存在內在聯繫,而且兩者的誤差是可以計算出來的,因此提供了用實際調查部分信息對總體數量特徵進行推斷的科學方法。
(3)抽樣誤差可以事先計算並加以控制。以樣本資料對總體數量特徵進行推斷,不可避免會產生代表誤差,但抽樣調查的代表性誤差是可以根據有關資料事先計算並進行控制,故可以保證推斷結果達到預期的可靠程度。
隨機抽樣最主要的優點是,由於每個樣本單位都是隨機抽取的,根據概率論不僅能夠用樣本統計量對總體參數進行估計,還能計算出抽樣誤差,從而得到對總體目標變數進行推斷的可靠程度。但隨機抽樣比較複雜,對調查人員的專業技術要求高,調查中需要抽樣框,而構建和維護一個高質量的抽樣框費用很高,抽樣單位可能非常分散,而且不能輕易更換樣本單位,增加了調查費用。
又稱簡單隨機抽樣。是最基本的抽樣方法。分為重複抽樣和不重複抽樣。在重複抽樣中,每次抽中的單位仍放回總體,樣本中的單位可能不止一次被抽中。不重複抽樣中,抽中的單位不再放回總體,樣本中的單位只能抽中一次。社會調查採用不重複抽樣。
純隨機抽樣的具體作法有:①抽籤法。將總體的全部單位逐一作簽,攪拌均勻後進行抽取。②隨機數字錶法。將總體所有單位編號,然後從隨機數字錶中一個隨機起點(任一排或一列),開始從左向右或從右向左、向上或向下抽取,直到達到所需的樣本容量為止。
純隨機抽樣必須有一個完整的抽樣框,即總體各單位的清單。總體太大時,製作這樣的抽樣框工作量巨大,加之有許多情況,使總體名單根本無法得到。故在大規模社會調查中很少採用純隨機抽樣。
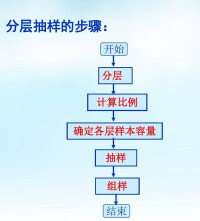
分層抽樣
先依據一種或幾種特徵將總體分為若干個子總體,每一子總體稱作一個層;然後從每層中隨機抽取一個子樣本,這些子樣本合起來就是總體的樣本。各層樣本數的確定方法有 3種:①分層定比。即各層樣本數與該層總體數的比值相等。例如,樣本大小n=50,總體N=500,則n/N=0.1即為樣本比例,每層均按這個比例確定該層樣本數。②奈曼法。即各層應抽樣本數與該層總體數及其標準差的積成正比。③非比例分配法。當某個層次包含的個案數在總體中所佔比例太小時,為使該層的特徵在樣本中得到足夠的反映,可人為地適當增加該層樣本數在總體樣本中的比例。但這樣做會增加推論的複雜性。
總體中賴以進行分層的變數為分層變數,理想的分層變數是調查中要加以測量的變數或與其高度相關的變數。分層的原則是增加層內的同質性和層間的異質性。常見的分層變數有性別、年齡、教育、職業等。分層隨機抽樣在實際抽樣調查中廣泛使用,在同樣樣本容量的情況下,它比純隨機抽樣的精度高,此外管理方便,費用少,效度高。
又稱等距抽樣。是純隨機抽樣的變種。在系統抽樣中,先將總體從1~N相繼編號,並計算抽樣距離K=N/n。式中N為總體單位總數,n為樣本容量。然後在1~K中抽一隨機數k1,作為樣本的第一個單位,接著取k1+K,k1+2K……,直至抽夠n個單位為止。
系統抽樣要防止周期性偏差,因為它會降低樣本的代表性。例如,軍隊人員名單通常按班排列,10人一班,班長排第 1名,若抽樣距離也取10時,則樣本或全由士兵組成或全由班長組成。
簡單的一個例子:在100個人里要抽10個人,現把他們從1號編到100號,然後分成1-10號, 11-20號, 21-30號, 31-40號, 41-50號。。。。。。91號到100號。在這10組中,第一組抽3號(其實可以選1-10號里的任意一號)。那麼第2組抽13號,第3組抽23號,第4組抽33號。。。第10組抽93號。
又稱聚類抽樣。先將總體按照某種標準分群,每個群為一個抽樣單位,用隨機的方法從中抽取若干群,抽中的樣本群中所有單位都要進行調查。與分層抽樣相反,整群抽樣的分類原則是使群間異質性小,群內異質性大。分層抽樣時各群(層)都有樣本,整群抽樣時只有部分群有樣本。整群抽樣只需列出入樣群的單位,因此可節約大量財力、人力。整群抽樣的代表性低於簡單隨機抽樣。
又稱多級抽樣。前 4種抽樣方法均為一次性直接從總體中抽出樣本,稱為單階段抽樣。多階段抽樣則是將抽樣過程分為幾個階段,結合使用上述方法中的兩種或數種。例如,先用整群抽樣法從北京市某中等學校中抽出樣本學校,再用整群抽樣法從樣本學校抽選樣本班級,最後用系統或純隨機抽樣從樣本班級的學生中抽出樣本學生。當研究總體廣泛且分散時,多採用多階段抽樣,以降低調查費用。但由於每級抽樣都會產生誤差,經過多級抽樣產生的樣本,誤差也相應增大。
單純隨機抽樣有不少優點,主要有:
第一,單純隨機抽樣方法簡單、直觀,是隨機抽樣理論中最基本的組織形式,是抽樣理論的基石。例如,日常生活中經常進行的挑選購物,某種商品短缺時的抓鬮認購等,均是單純隨機抽樣的簡單原型。
第二,單純隨機抽樣是其他抽樣方式的基礎,即隨機抽樣的各種組織形式都是單純隨機抽樣的派生方式。例如,整群抽樣即是把某一標誌下性質相同的一些總體單位構成的群體或組視為一個個體,然後進行單純隨機抽樣,其中的分群工作並不具有隨機性,僅是分群前提下的隨機抽樣。
第三,單純隨機抽樣是衡量各種抽樣方式效果好壞的一個比較標準。用樣本指標估計、推斷相應的總體指標,隨著所採取的組織形式的不同,其對同一個調查指標估計結果的有效程度就不同。
第一,採用單純隨機抽樣,一般需要對總體單位加以編號,而當總體包含的個體數目很大時,編號工作就很困難,逐一編號無法做到。例如,對於連續不斷生產的大量產品進行質量檢驗,就不能對全部產品進行編號抽樣。
第二,當總體的標誌變異程度較大,即總體單位標誌值之間差異很大時,單純隨機抽樣的代表性就不如經過分層后再抽樣的代表性高(詳見以下的“分層抽樣”)。
第三,當調查對象範圍很廣,即總體中各單位較為分散時,調查所需的人力、物力、財力就較大。因此,單純隨機抽樣適用於總體容量不太龐大,以及總體分佈比較均勻的調查對象。
