擴散超電勢
擴散超電勢
物質在液相中的傳遞有三種形式:①遷移,這是電場引起的帶電物種的傳遞過程,通過在電解液中加入過量的非電極活性的“無關電解質”,電極活性物質的遷移可以得到抑制;②對流,這是溶液本身的流動引起的物質傳遞過程, 對流過程可利用轉盤電極精確控制(見穩態技術);③擴散,這是溶液中存在濃差而引起的物質傳遞過程,是這裡要討論的主題。
I1=-FDcb/δ(4)
由於Ag+電沉積的遷越過程中I0很大,可認為是可逆的,故可以利用能斯脫平衡電勢公式來推導擴散步驟的超電勢ηd:
(5)此式是上述電積過程的擴散超電勢的表達式,其特徵是存在著極限電流I1。極限電流限制了實際的生產過程,但通過攪拌可以減小有效擴散層厚度δ,增加I1以強化生產過程。
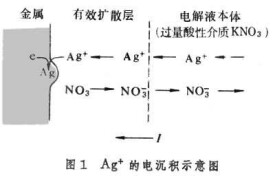
對於電極反應,現考慮Ag+的電沉積過程:
Ag++e─→Ag (1)
它的遷越步驟交換速率很快,即交換電流密度I0很大,故要求的推動力很小,因此遷越超電勢ηCT→0。在過量的“無關電解質”存在的條件下,電極的電流I完全靠Ag+的擴散步驟來支持(圖1),即決定於Ag+到達金屬相表面的擴散通量ФAg+。
根據法拉第電解定律和斐克第一定律(見擴散),可得下式:
(2)
式(2)的負號表示還原電流有負值,D為擴散係數,F為法拉第常數。為了找出界面的濃度梯度дc/дx,W.H.能斯脫於1904年提出了一個近似的假設,即在電極的液相界面上存在著有效擴散層,它的厚度為δ(約10~100微米)。在該層的內部,濃度梯度是線性的(圖 2);在該層之外,Ag+的濃度與溶液本體濃度cb一樣。能斯脫的上述模型雖與實際不盡相符,但使問題的處理大為簡化,且所得結果與比較嚴格的處理相差不大。這樣,式(2)可簡化為:
(3)
式中的cS表示Ag+在金屬表面的濃度。
當上述電極極化增大時,電流增加使金屬表面Ag+的沉積加速,最終cS將降到零,產生極限電流。此時有效擴散層中的濃度梯度達到最大,ФAg+已不再能增加,使電流達到極限值I1(圖3)。則得: