中位線定理
描述平面幾何線段間關係的定理
中位線是在三角形或梯形中一條特殊的線段，與其所在的三角形或梯形有著特殊的關係。連接三角形的兩邊中點的線段叫做三角形的中位線。三角形有三條中位線，首尾相接時，每個小三角形面積都等於原三角形的四分之一，這四個三角形都互相全等。
（1）三角形中位線定義：連接三角形兩邊中點的線段叫做三角形的中位線。
（2）梯形中位線定義：連接梯形兩腰中點的線段叫做梯形的中位線。
（1）要把三角形的中位線與三角形的中線區分開。三角形中線是連接一頂點和它的對邊中點的線段，而三角形中位線是連接三角形兩邊中點的線段。
（2）梯形的中位線是連接兩腰中點的線段而不是連結兩底中點的線段。
（3）兩個中位線定義間的聯繫：可以把三角形看成是上底為零時的梯形，這時三角形的中位線就變成梯形的中位線。
（1）三角形中位線定理：三角形的中位線平行於第三邊並且等於它的一半．
（2）梯形中位線定理：梯形的中位線平行於兩底，並且等於兩底和的一半．
中位線定理證明
求證：DE∥BC DE=1/2 BC
證明：延長DE至F，使EF=DE，連接CF
∵DE是△ABC的中位線
∴AE=CE
在△ADE和△CFE中
∵AE=CE（已證），∠AED=∠CEF（對頂角相等），DE=EF（已作）
∴△ADE≌△CFE（SAS)
∴AD=CF（全等三角形對應邊相等）
∠ADE=∠F（全等三角形對應角相等）
∴BD∥CF（內錯角相等，兩直線平行）
∵AD=BD
∴BD=CF
∴四邊形BCFD是平行四邊形
∴DE//BC，DE=1/2DF=1/2BC
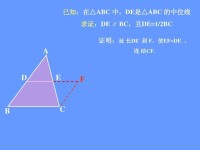
已知△ABC中，D、E分別是AB、AC兩邊中點。
求證DE平行於BC且等於BC/2
方法一：幾何法
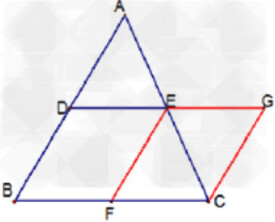
過C作AB的平行線交DE的延長線於G點。
∵CG∥AD
∴∠A=∠ACG
∵∠AED=∠CEG、AE=CE、∠A=∠ACG（用大括弧）
∴△ADE≌△CGE （A.S.A)
∴AD=CG（全等三角形對應邊相等）
∵D為AB中點
∴AD=BD
∴BD=CG
又∵BD∥CG
∴BCGD是平行四邊形（一組對邊平行且相等的四邊形是平行四邊形）
∴DG∥BC且DG=BC
∵△ADE≌△CGE （A.S.A)
∴DE=GE
∴DE=DG/2=BC/2
∴三角形的中位線定理成立
方法二：坐標法
設三角形三點分別為（x1，y1），（x2，y2），（x3，y3）
則一條邊長為：根號（x2-x1）^2+(y2-y1）²
另兩邊中點為（（x1+x3）/2，（y1+y3）/2），和（(x2+x3）/2，（y2+y3）/2）
這兩中點距離為：根號（（x2+x3）/2-(x1+x3）/2）^2+((y2+y3）/2-(y1+y3）/2）^2
最後化簡時將x3，y3消掉正好中位線長為其對應邊長的一半
方法三
延長DE到點G，使EG=DE，連接CG
∵點E是AC中點
∴AE=CE
∵AE=CE、∠AED=∠CEF、DE=GE
∴△ADE≌△CGE (S.A.S)
∴AD=CG、∠G=∠ADE
∵D為AB中點
∴AD=BD
∴BD=CG
∵點D在邊AB上
∴DB∥CG
∴BCGD是平行四邊形
∴DE=DG/2=BC/2
∴三角形的中位線定理成立
方法四：向量DE=DA+AE=(BA+AC)/2=BC/2
∴DE//BC且DE=BC/2
基本信息
- 中文名
- 中位線定理
- 外文名
- Median line theorem
- 應用學科
- 數學
- 適用領域
- 平面幾何線段間的關係
- 表達式
- 三角形的中位線平行於第三邊並且等於它的一半