泊肅葉定律
泊肅葉定律
實驗表明,流體在水平圓管中作層流運動時,其體積流量Q與管子兩端的壓強差Δp,管的半徑r,長度L,以及流體的粘滯係數η有以下關係:
Q徠=π×r^4×Δp/(8ηL)
這就著名的泊肅葉定律(Poiseuille定律)。令R=8ηL/(πr^4),即Q=Δp/R,R稱為流阻。
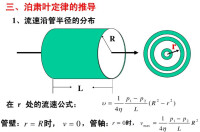
泊肅葉定律
可對 泊肅葉定律作進一步討論:
(1)流阻R與管子半徑r的四次方成反比。這說明,管子的半徑對流阻的影響非常大。例如,在管子長度、壓強差等相同的情況下,要使半徑為r/2的管子與半徑為r的管子有相同的流量,並聯細管的根數需要2^4,即16根。
(2)流阻R與管子的長度L成正比。管子越長,流阻越大。
(3)流阻R與液體的粘滯係數η成正比。液體的粘滯係數越大,流阻就越大。
由此可見,流量Q是由液體的粘滯係數η、管子的幾何形狀和管子兩端壓強差ΔP等因素共同決定的。
泊肅葉定律可以近似地用於討論人體的血液流動。但應指出,由於血管具有彈性,與剛性的管子不同,其半徑是可變的,因此流阻會隨血管半徑的變化而變化,這一變化也會影響到血液的流量Q。
泊肅葉定律(Poiseuilelaw)Q=πr^4xΔP/8ηl(1)是描述不可壓縮的粘性流體在水平圓管中作定常流動,且雷諾數不大,流動的形態是層流時,流量Q與管道兩端的壓力差ΔP、管道半徑r0、管道長度l及流體粘度係數η的關係。泊肅葉定律是流體動力學的一個重要定律,常用於測定流體的粘滯係數、血液流動分析、藥物分析和製劑中,是醫學生和藥學生感興趣的物理知識。遵循定律的適用條件,科學地使用泊肅葉定律,將促進醫學、藥學的研究和發展。本文將對泊肅葉公式的適用條件,泊肅葉公式在血流動力學徠應用中有關。
