交換律

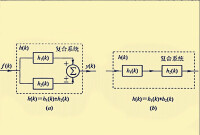
圖1 並聯與級聯複合系統

交換律是離散信號卷積和運算最常用的幾個基本運算規則之一，離散序列卷和運算滿足交換律，即兩序列卷和運算與卷和次序無關，即。

與連續信號卷積積分運算規則對照，離散序列信號卷積和運算也有相應的一些運算規則，不過卷積和的差分規則、累和規則用得很少，常用的離散信號卷積和運算的幾個基本運算規則是交換律，結合律和分配律。

卷和運算的交換律、結合律、分配律可仿照卷積運算的交換律、結合律、分配律推導過程證明成立，這裡應強調的是，結合律與分配律應用於系統分析時主要用來等效化簡複合系統：兩個子系統並聯組成的複合系統，其單位序列響應等於相併兩子系統單位序列響應的代數和。如圖1中（a）所示。兩個子系統級聯組成的複合系統，其單位序列響應等於相級聯兩子系統單位序列響應的卷積和，如圖1中（b）所示。

三個序列卷和運算，任意兩個序列先卷和運算，再與第3個序列作卷和運算，其運算結果等同，即。

兩個序列先行相加運算再與第3個序列做卷和運算，其結果等於這兩個序列分別與第3個序列先做卷和運算，然後二者再相加。即。

與連續時間信號的卷積積分相對應和類似，離散信號有卷積和的運算。其定義為。

圖2

與卷積分的性質相對應和類似，卷積和也有一些同樣的性質，如圖2所示；

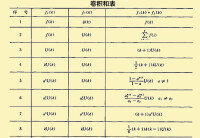
圖3 卷積和表

常用信號的卷積和如圖3所示；

求卷積和常用方法

(1)單位序列卷積和法；

(2)直接求累加和法；

(3)圖解法；

(4)解析法(配合查卷積和表)；

(5)排表法；

(6)利用差分性質求。

結合律和交換律密切相關著。結合律是指運算的順序並不會影響其最終結果。相對地，交換律則是指運算元的順序不會影響其最終結果的性質。

對稱可以和交換律有直接的關連。若將一個可交換運運算元寫成一個二元函數，則此一函數會對 y = x 這條線對稱。舉例來說，若設一函數 f 來表示加法（一可交換運算），所以 f(x,y) = x + y 。

​