對數式
對數式
對數式(logarithmic expression)是一類特殊的解析式，指含有對未知數進行對數運算的解析式，如log2(x-1)，logax+b都是關於x的對數式，簡稱對數式。
定理 如果a是一個不等於1的正實數，那麼對於任意給定的正實數N，都存在惟一的實數b，使得a =N。
定義 設a是一個不等於1的正實數，N是任意給定的正實數，如果實數b使得等式a =N成立，那麼b叫做以a為底的N的對數，記作logN=b，N叫做真數。
根據對數定義，指數式a =N和對數式logN=b是等價的。在處理有關問題時，它們可以互相轉化，從而簡化解題過程。
對數有以下幾個主要性質，其中a>0，a≠1，M>0，N>0 。
1．基本性質
性質1 零和負數沒有對數。
性質2 底的對數等於1，loga=1。
性質3 1的對數等於0，log1=0。
2．運算性質
性質4 log(MN)=logM+logN。
性質5 log(M/N)=logM-logN。
性質6 logN =nlogN。
3．常用恆等式
對數式
對數式
對數式
對數式
對數式
對數式
對數式
【例1】已知，求
對數式
對數式
對數式
對數式
證明：由已知得，即 且，即
對數式
對數式
對數式
【例2】已知求證
證明：設已知比例式的比值為k，得
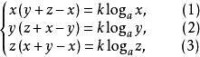
對數式
對數式
以得
對數式
對數式
對數式
注意到均為不等於1的正整數，所以，由上式可知
對數式
對數式
對數式
基本信息
- 外文名
- logarithmic expression
- 所屬學科
- 數學
- 所屬問題
- 初等代數（對數）
- 簡介
- 有對未知數進行對數運算的解析式