節約里程法
解決運輸車輛數目問題的演演算法
節約里程法是用來解決運輸車輛數目不確定的問題的最有名的啟髮式演演算法。又稱節約演演算法或節約法,可以用并行方式和串列方式來優化行車距離。
節約里程法核心思想是依次將運輸問題中的兩個迴路合併為一個迴路,每次使合併后的總運輸距離減小的幅度最大,直到達到一輛車的裝載限制時,再進行下一輛車的優化。優化過程分為并行方式和串列方式兩種。
利用節約法確定配送路線的主要出發點是,根據配送中心的運輸能力和配送中心到各個用戶以及各個用戶之間的距離來制定使總的車輛運輸的噸公里數最小的配送方案。另還需滿足以下條件;(1)所有用戶的要求;(2)不使任何一輛車超載;(3)每輛車每天的總運行時間或行駛里程不超過規定的上限;(4)用戶到貨時間要求。
為達到高效率的配送,使配送的時間最小距離最短成本最低,而尋找的最佳配送路線。
計算方法如下圖,假設O點為配送中心,它分別向地點A和B送貨。設O點到地點A和地點B的距離分別為a和b。地點A和地點B之間的距離為c,現有兩種運輸方案,如圖下(a)和(b)所示。
圖(a) 兩個地點單獨運輸
計算公式圖a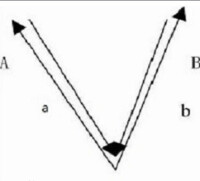

節約里程法
圖(b)兩個地點合成一個迴路進行運輸
計算公式圖b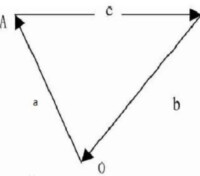

節約里程法
容易得到:
在上圖(a)中運輸距離為2(a+b);圖上(b)中運輸距離為a+b+c;
合併后的總運輸距離之差為:
2(a+b)-(a+b+c)=(2a+2b)-a-b-c=a+b-c
即得到計算公式是兩點到中心的距離和減去兩點間距離。
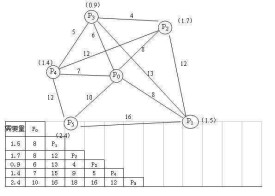
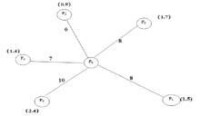
例題:已知配送中心P0向5個用戶Pj配送貨物,其配送路線網路、配送中心與用戶的距離以及用戶之間的距離如下圖所示,配送中心有3台2t卡車和2台4t兩種車輛可供使用。利用節約里程法制定最優的配送方案。
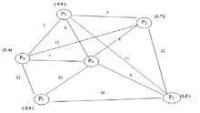
節約里程法例題用圖

節約里程法
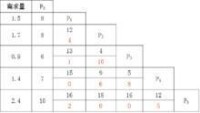
節約里程法
節約里程法
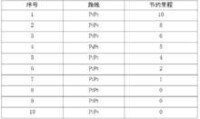
P2P3-P3P4-P2P4-P4P5-P1P2-P1P5-P1P3-P2P5-P3P5-P1P4
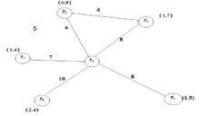
節約里程法

節約里程法
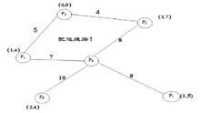
節約里程法
得出結果:
配送線路一:
運量=1.7+0.9+1.4=4t
運行距離=8+4+5+7=24km
用一輛4t車運送,節約距離為18km
配送線路二:
運量=2.4+1.5=3.9t<4t
運行距離=8+10+16=34km
用一輛4t車運送,節約距離為2km
節約里程法
優化后的方案:2條配送路線,2輛4t車,配送距離=24+34=58km