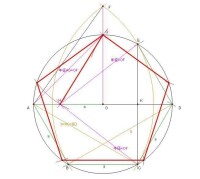
五等分圓周
分割圓形的方法
五等分圓周,是一種分割圓形的方法。
作法(一):單規作圖法--只能用圓規, 不能用直尺
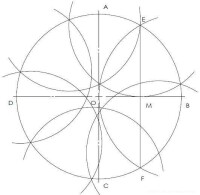
五等分圓周
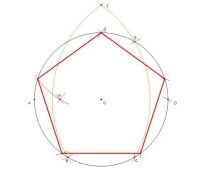
⑴ 以 a 為半徑在圓上相繼取相等的弧 AB, BC, CD 和 DE.
⑵ 以 AC 為半徑, A 和 D 分別為圓心, 作弧相交於 F.
⑶ 以 OF 為半徑, A 為圓心作弧交圓 O 於 G.
⑷ 仍以 OF 為半徑, 分別以 C 和 E 為圓心, 作弧交於 H.
GH 即是內接正五邊形的邊長, 以圓上任意一點開始, GH 為半徑, 相繼在圓上取 5 個點, 這 5 個點就可以五等分圓.
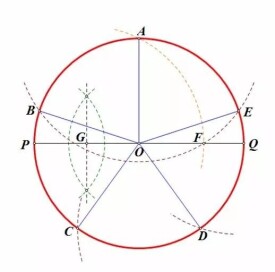
作法(二): 尺規作圖法
以 O 為圓心, a 為半徑作一個圓.
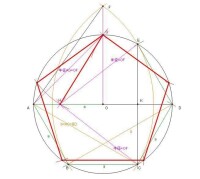
⑴ 作直徑AD和半徑OG,使OG⊥AD.
⑵ 作OD的中點K.(OK=a/2)
⑶以 K為圓心, KG為半徑作弧交AD於H.(HK=KG=a√5/2)
易求得HO = HK - OK = a√5/2 - a/2 = (√5-1)a/2,GH=a√((5-√5)/2)
∴GH 即是內接正五邊形的邊長, 以圓上任意一點開始, GH 為半徑, 相繼在圓上取 5 個點, 這 5 個點就可以五等分圓
OD, CE 相交於 K,
以下事實是容易證明的:
A, O, D, H 共線;
AC = a√3; (AC 實為 3 等分圓的取點半徑, 對應圓心角為 120°)
AG = OF = a√2; (見詳證●)
G 在 OF 上, 且 OG ⊥ OA; (見詳證●)
HK² = CH² - CK² = 2a² - 3a²/4 = 5a²/4; (見詳證①)
HK = a√5/2;
HO = (√5-1)a/2. (見詳證②)
因此, HO 長是圓的內接正十邊形的邊長(見詳證③ 第1.節)
在半徑為 a 的圓中, 內接正五邊形的邊長(見詳證③ 第2.節)
m = a√((5-√5)/2)
m² = a²(5-√5)/2
GH² = HO² + OG² = ((√5-1)a/2)² + a² = a²(6-2√5)/4 + a² = a²(5-√5)/2
∴ GH = m, 即 GH 為內接正五邊形的邊長
以下為中間過程或引理詳細證明:
●證明:
由作法易知, A, B, C, D, E 都是圓的 6 等分點, AD 為直徑,
由 F 的作法易證 OF ⊥ AD (AF = DF => △FAD 為等腰三角形, 底邊 AD 的中線 OF 必也是高),
AF = AC = a√3,
∴ OF² = AF² - AO² = (a√3)² - a² = 2a² => OF = a√2.
由作法知
AG = OF = a√2
AG² = 2a² = OA² + OG²
∠AOG 必為 90°(用勾股定理逆定理證 △AOG 為 Rt△)
∴ G 在 OF 上, 且 OG ⊥ OA;
①證明
CK = AC * sin∠COD = AC * sin30° = a√3 * 1/2 = a√3/2
②證明
易證 CE 垂直平分 OD, 所以 OK = a/2
HO = HK - OK = a√5/2 - a/2 = (√5-1)a/2
③證明: 在半徑為 a 的圓中,
1. 內接正十邊形的邊長為 a(√5-1)/2.
2. 內接正五邊形的邊長為 a√((5-√5)/2).
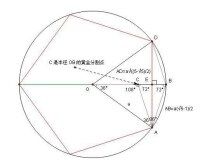
如圖, ⊙O 的半徑為 a, 圓周上 A, B, D 都是圓周上的十等分點,
AD 為內接正五邊形的一條邊, 交 OB 於 E.
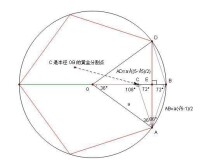
五等分圓周
易知兩半徑 OA, OB 所夾圓心角 ∠AOB = 36°,
作 ∠OAB 的角平線交 OB 於 C
易證如下事實:
∠OAC = ∠COB = ∠AOB = 36°;
∠OBA = ∠ACB = 72°;
BC 與 AD 互相垂直平分;
OC = CA = AB = L (設 L 為圓的內接正十邊形的邊長)
△ACB ∽ △OAB
=> OA:AC = AB:CB
又 CB = OB - OC
∴ a:L = L:(a - L)
L² = a (a-L)
解此方程得正解
L = a(√5-1)/2.
(PS: 事實上, 圖中 C 正是半徑 OB 的黃金分割點)
2. 內接正五邊形的邊長為 a√((5-√5)/2)
根據相似三角形比例關係可得
BC = AB (√5-1)/2 = a(√5-1)/2 * (√5-1)/2 = a(3-√5)/2
BE = BC/2 = a(3-√5)/2/2 = a(3-√5)/4
AE² = AB² - BE²
AD² = (2AE)² = 4AE² = 4AB² - 4BE²
= 4(a(√5-1)/2)² - 4(a(3-√5)/4)²
= a²(5-√5)/2
∴ AD = a√((5-√5)/2)
五等分圓周
五等分圓周
五等分圓周