有理數集

有理數集，即由所有有理數所構成的集合，用黑體字母Q表示。有理數集是實數集的子集

有理數集是一個無窮集，不存在最大值或最小值。

集集集。容系擴。

集語/語（商）首，整商。

集域，即則運算（除除），且運算，運算律成立（a、b、c等都表示任意的有理數）

● ● 加法的交換律：

● ● 加法的結合律：

● ● 存在加法的單位元0使

● ● 對任意有理數a，存在一個加法逆元，記作-a，使

● ● 乘法的交換律：

● ● 乘法的結合律；【

● ● 乘法的分配律：

● ● 存在乘法的單位元1，使得對任意有理數a，有

● ● 對於不為0的有理數a，存在乘法逆元

● ● 說明：一個數乘0還等於0。

此外，有理數是一個序域，即在其上存在一個次序關係：≤

由於有理數集中所有元素均為有理數，因此可得：

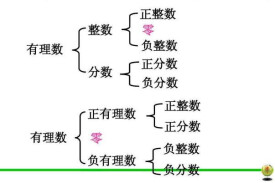
• 整數集、分數集、小數集、自然數集，都是有理數集的一個子集

• 即：有理數包含整數、分數、小數、自然數等（不考慮重複列舉關係）

• 有理數集是實數集的一個子集，也是複數集的一個子集

• 即：有理數是實數（或複數）的一部分