共找到2條詞條名為勢函數的結果 展開
- 勢函數
- 功效函數
勢函數
勢函數
勢函數的構造是人工勢場方法中的關鍵問題,典型的勢函數構造方法:p(θ)=fd(θ,θ0),d[R(θ),O],dT(1),式中θ,θ0——機器人當前位姿與目標位姿矢量;d(θ,θ0)——θ與θ0間的某種廣義距離函數;d[R(θ),O]——當前位姿下機器人與障礙物間的最小距離;dT——給定的門限值;P(θ)分別為變數d(θ,θ0)和d[R(θ),O]的單調遞增函數和單調遞減函數。從機器人的起始位姿開始沿著P(θ)的下降方向進行搜索可使機器人在避開障礙物的前提下向目標位姿運動。
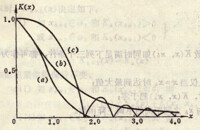
勢函數法
基於L1距離的人工勢函數構造與無碰撞路徑規劃方法滿足條件以R(θ),O分別表示機器人及其操作空間中的障礙物,其中R(θ)決定於機器人的C-空間位姿矢量θ。所謂無碰撞路徑規劃,就是確定一條連接C-空間中起始位姿θi和目標位姿θO的連續路徑S(θi,θO),使得機器人沿該路徑運動時,在其所有的中間位姿θ∈S(θi,θO)滿足如下幾何約束條件⑽為了將上述約束條件表示成便於計算機判別的形式,通常採用如下形式的凸多面體集合對機器人及其操作空間中的障礙物進行幾何逼近⑾式中Ri(θ)(i=1,…,m),Oj(j=1,…,l)為R3中的凸多面體。機器人與障礙物間的L1距離可按下式由各多面體對Ri(θ),Oj間的L1距離確定⑿且根據L1距離的拓撲性質,幾何約束條件式⑽可等價地表示成d1[R(θ),O]>0 ⒀以θi,θO∈Rn分別表示n自由度機器人的起始位姿和目標位姿。定義機器人運動過程中任意中間位姿θ∈Rn與目標位姿之間的廣義距離為(W∈Rn×n為正定加權矩陣)⒁按如下方法構造C-空間中的勢函數⒂由式⒂所確定的勢函數p(θ)具有如下特點:⑴當機器人與障礙物間的L1距離大於門限值dT時,勢函數的值由當前位姿與目標位姿間的廣義距離d(θ,θO)確定,此時機器人只受到目標位姿引力場的作用。⑵當機器人與障礙物的L1距離小於門限值dT時,人工勢場由目標位姿的引力場和障礙物的斥力場兩部分組成,其中障礙物的斥力場所對應的勢函數分量反比於機器人與障礙物間的L1距離,因此當機器人與障礙物間的L1距離趨於零時,該分量的值趨於無窮大。⑶勢函數的值可由式⑼、⑿、⒁、⒂以及機器人正向運動學方程計算。搜索方法從機器人在C-空間中的起始位姿開始,沿著人工勢函數p(θ)的下降方向進行搜索,可以得到C-空間中滿足幾何約束條件式⑽的連續路徑。我們分d1[R(θ),O]>dT和d1[R(θ),O]?dT兩種情況討論無碰撞路徑搜索方法。⑴若d1[R(θ),O]>dT,則勢函數p(θ)關於θ可微,並有⒃此時可按勢函數的最速下降方向,即其負梯度方向-?p(θ)搜索機器人的下一個位姿點。對於搜索得到的位姿點,判斷條件d1[R(θ),O]>dT是否滿足,若是,則以該點作為起始點重複以上搜索過程,否則改用下面的方法進行搜索。⑵若d1[R(θ),O]?dT,則勢函數p(θ)不存在Frechet意義下的梯度向量,此時由於得不到最速下降方向,因此採用如下的搜索策略;對於θ的各相鄰位姿θ+δθ(δθ∈Δ),計算勢函數p(θ+δθ)的值,其中⒄為容許的搜索步長集合。按下式確定⒅若,則終止搜索。若,判斷條件,dT是否滿足,若是則以作為起始點重複上述搜索,否則改用最速下降方法進行搜索。產生結果採用以上搜索方法可能產生兩種不同的結果:一是搜索過程終止於目標位姿,此時已經得到C-空間中的連接起始位姿和目標位姿的無碰撞路徑,規劃完成。另一種可能的結果是在到達目標位姿之前,搜索過程終止於人工勢函數的局部極小點,此時勢函數無下降方向,必須採用其他方法才能使搜索過程繼續下去。有關人工勢函數的局部極值處理目前已有許多研究,此處不再介紹。一般說來,若搜索步長足夠小,則儘管規劃過程中只順序搜索C-空間中一些離散位姿點,但L1距離的Lipschitz性足以保證規劃出的路徑滿足幾何約束條件。但減小搜索步長是以增加演演算法的計算複雜性為代價的,為簡化計算,搜索過程中可以根據當前位姿下機器人與障礙物間的L1距離大小對步長進行調整。對於由上述方法規劃出的C-空間位姿序列,採用適當的方法進行插補即可得到連續的無碰撞路徑。
圖形模擬
平面3自由度機器人路徑規劃模擬結果圖示平面移動機器人具有3自由度,選擇端點A的坐標以及AB與參考坐標系x軸的夾角構成C-空間位姿矢量[xA,yA,φ]T,記AB的長度為lAB,則端點B的坐標可由如下運動學方程計算⒆給定機器人的起始位姿和目標位姿(如圖示),以及障礙物Oi(i=1,2,3,4)的頂點集,採用本文給出的無碰撞路徑規劃方法,得到圖示結果。
結論