共找到18條詞條名為丁鋒的結果 展開
丁鋒
青年設計理論研究者
男,漢族,山東泰安人,平面設計工作者,碩士學歷,中國包裝總公司包裝設計技術專業中心成員。主要從事格式塔心理學理論與平面設計方面的研究。近幾年先後參與國家級和省級課題4項,發表論文5篇,並在取得多項獎勵。
論文《格式塔心理學理論研究之小議殘缺之美》發表於《藝術與設計》;
論文《日本設計大師五十嵐威暢字體設計淺析》發表於發表於《藝術探索》;
論文《埃舍爾契合形之構圖規律淺析》收錄於《綠色之辯論文集》並發表於《包 裝學報》;
論文《欣賞是一種創造》發表於《藝術空間》;
論文《深澤直人與他的“無意識設計”》發表於《新視覺藝術》。
參與湖南省軟科學研究計劃項目《產學研模式下的飲食陶瓷產品開發及包裝設計戰略研究》;《藝術設計學專業藝術設計基礎課程教學改革研究》;《中國傳統裝飾紋樣藝術符號研究》等。
承接中國包裝總公司包裝設計技術專業中心網站建設;湖南工業大學科技處網站建設等。
1、何為契合
在中國漢語中“契合”有三種解釋:①投合,意氣相投;②符合;③結盟,結拜。在平面藝術設計中我們主要是取其“②符合”之意,就是幾個圖形輪廓完全符合,達到圖底基本形輪廓上的完美結合。日本設計教育家朝倉直巳的《藝術·設計的平面構成》中被譯者譯為“瓷磚式分割”。在荷蘭著名的版畫大師埃舍爾那裡是作為“周期性圖形分割”(Periodic Drawing Division)的鑲嵌圖形進行探討的,他把“規則鑲嵌”(Regular Tessellation,也就是本文的契合形)讚美為:“這是我挖掘出來的最豐富的靈感之泉,它至今也沒有枯竭。”契合形由來久已,中國的太極圖便是其典型的例證,西班牙的阿爾漢布拉宮 [注1]中也不乏契合形的優秀作品。
契合形大抵可分為兩類:狹義的契合形,如埃舍爾的作品中表現的大部分契合形,也可以稱作繁殖性契合形;廣義的契合形,只要有契合之處,則為契合之形,此類實例多體現於建築設計、室內設計及產品設計中。文章將以埃舍爾的繁殖性契合形為切入點,根據它們的各自特點,對它們進行分類解構,分析其成因與製作方法,探索它們的潛在的構圖規律。
2、契合形的構圖規律

圖1 鳥、魚、龜埃舍爾 張小華繪製
在分析前,筆者認為有必要先區分一下“契合元素”、“基本形”與“契合骨骼單元”這三個概念。以埃舍爾的《鳥、魚、龜》為例(見圖1所示),契合元素”為契合形中構圖的基本元素(如圖1中的鳥、魚、龜);“基本形”為契合形骨架中最基本的構成元素(如圖1中的三角形);一副契合作品中會存在一個甚至幾個不同的“基本形”,而由基本形構成的“契合骨骼單元”包含著契合形中所有的元素,如圖1中的任意一個由6個“基本形”(三角形)組成的正六邊形,就是1個“契合骨骼單元”(文中簡稱單元)。
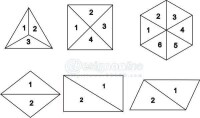
圖2 契合“基本形”分析圖 丁鋒繪製
2.1 三角形契合

圖3 蜥蜴、魚、蝙蝠 埃舍爾 製作:丁鋒

圖4 蝴蝶 埃舍爾 分析製作:丁鋒

圖5 騎士 埃舍爾 分析製作:丁鋒

圖6 魚和船 埃舍爾 分析製作:丁鋒
2.1.3反轉對稱契合 前文已經提到,太極圖為一種典型的契合圖形,但並非文中所說的繁殖性契合形,不過有些契合形在形體特徵上與太極圖有很大的相似之處,這種契合形多表現為兩種相同或者相似的元素環抱在一起,因兩個元素間是反轉對稱的關係,因此稱作反轉對稱契合。這種契合形可以依照半體錯位契合的規律,也可以依照重複旋轉契合的方式來進行解構分析。如圖7A所示,兩個魚環抱在一起形成一對反轉對稱,下面我們將以半體錯位契合圖形的解構方法,對其進行解構分析。首先我們對圖像進行去色,找出基本形,如圖7C,然後將兩個基本形錯位排列,構成單元,本契合形便是由此契合單元排列而成的。

圖7 飛魚 埃舍爾 分析製作:丁鋒
2.2 三角形組構契合
前文提到契合形的基本形一般就是三角形,但是並不是所有的契合形都符合這個規律,而是在這個規律的基礎上進行了適當的延伸,即為以兩個或者多個三角形構成的圖形作為一個契合單元進行組構結合而成的,這類圖形根據契合單元的數目和契合單元的方向可以分為單行單向、單行雙向、單行四向、單行六向、雙形雙向、雙形四向、雙形六向契合,其中單行單向、單行雙向、單行六向、雙形雙向、雙形六向契合均可按照三角形契合的規律進行解構。

圖8 魚 埃舍爾 分析製作:丁鋒
因契合形本身的複雜性,以上幾種契合方式並不能涵蓋所有的契合形,但是只要是由一個或者幾個契合單元重複排列成的契合形一般都符合以上規律,而我們對其解構的方法均可按照先分類,然後找出基本形,組構出契合單元的方式進行。至於契合形的創作,我們可以反其道而行之,首先確定要表現的主題元素,然後觀察其最符合以上哪種契合方式,再將元素重複排列,套於契合框架中,從而抽象出基本形,完成契合形的創作過程。
2.3 偶然形契合

圖9 生靈 埃舍爾 分析製作:丁鋒
3、結語
契合形按其應用範圍可以分為狹義的契合形與廣義的契合形,而對於其圖形特徵的把握需以狹義契合形為切入點進行分析。埃舍爾的契合形融合了理性的思維也包含著感性的創造,有其特有的規律性,特別是那些具有繁殖性的契合形,其基本形一般就是三角形,是通過三角形的旋轉或錯位排列等方式構成基本的契合骨骼單元,而這類契合單元的重複和有秩序的排列,最終便完成契合形的創作。
因為契合形骨骼的不同,我們對其解構分析的方式也略有區別(而且還會根據不同的角度和視點會出現不同的解析方式),而依照解構方式的差異,契合形大體可以分為三角形契合、三角形組構契合以及偶然形契合,其中三角形契合又可以分為重複旋轉契合、半體錯位契合和反轉對稱契合。然而,對於契合形的解構均可依照先分析契合形,然後找出契合骨骼,再分解契合基本形,最後組構成契合骨骼單元,且凡是以繁殖元素重複排列的契合形一般都符合以上規律。