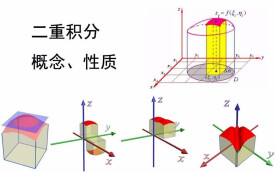
二重積分

設二元函數z=f（x，y）定義在有界閉區域D上，將區域D任意分成n個子域，並以 表示第個子域的面積。在 上任取一點作和。如果當各個子域的直徑中的最大值 趨於零時，此和式的極限存在，且該極限值與區域D的分法及的取法無關則稱此極限為函數 在區域上的二重積分，記為，即。

這時，稱 在上可積，其中 稱被積函數，稱為被積表達式，稱為面積元素，稱為積分區域，稱為二重積分號。

同時二重積分有著廣泛的應用，可以用來計算曲面的面積，平面薄片重心，平面薄片轉動慣量，平面薄片對質點的引力等等。此外二重積分在實際生活，比如無線電中也被廣泛應用。

性質1 （積分可加性）函數和（差）的二重積分等於各函數二重積分的和（差），即

性質2 （積分滿足數乘）被積函數的常係數因子可以提到積分號外，即

(k為常數）

性質3 如果在區域D上有f(x,y)≦g(x,y)，則

性質4 設M和m分別是函數f(x,y)在有界閉區域D上的最大值和最小值，σ為區域D的面積，

則

性質5 如果在有界閉區域D上f(x,y)=k（k為常數)，σ為D的面積，則Sσ=k∫∫dσ=kσ。

設函數f(x,y)在有界閉區域D上連續，σ為區域的面積，則在D上至少存在一點（ξ，η），使得

當被積函數大於零時，二重積分是柱體的體積。

當被積函數小於零時，二重積分是柱體體積負值。

在空間直角坐標系中，二重積分是各部分區域上柱體體積的代數和，在xoy平面上方的取正，在xoy平面下方的取負。某些特殊的被積函數f（x，y）的所表示的曲面和D底面所為圍的曲頂柱體的體積公式已知，可以用二重積分的幾何意義的來計算。

例如二重積分 ,其中，表示的是以上半球面為頂，半徑為a的圓為底面的一個曲頂柱體，這個二重積分即為半球體的體積。

二重積分和定積分一樣不是函數，而是一個數值。因此若一個連續函數f（x，y）內含有二重積分，對它進行二次積分，這個二重積分的具體數值便可以求解出來。

如函數，其積分區域D是由 所圍成的區域。

其中二重積分是一個常數，不妨設它為A。對等式兩端對D這個積分區域作二重定積分。

故這個函數的具體表達式為：f（x，y）=xy+，等式的右邊就是二重積分數值為A，而等式最左邊根據性質5，可化為常數A乘上積分區域的面積，將含有二重積分的等式可化為未知數A來求解。

當f（x，y）在區域D上可積時，其積分值與分割方法無關，可選用平行於坐標軸的兩組直線來分割D，這時每個小區域的面積Δσ=Δx·Δy，因此在直角坐標系下，面積元素dσ=dxdy，從而二重積分可以表示為

由此可以看出二重積分的值是被積函數和積分區域共同確定的。將上述二重積分化成兩次定積分的計算，稱之為：化二重積分為二次積分或累次積分。

設積分區域是由兩條直線x=a，x=b（a

特點：穿過D內部且平行於y軸的直線，與D的邊界不多於兩點。

如左圖，對任意取定的∈[a，b]，過點（，0，0）作垂直於x軸的平面，該平面與曲頂柱體相交所得截面是以區間 為底，z=f（，y)為曲邊的曲邊梯形，由於x0的任意性，這一截面的面積為，其中y是積分變數在積分過程中視x為常數。上述曲頂柱體可看成平行截面面積S（x）從a到b求定積分的體積，從而得到：

積分區域 稱為Y型區域。

特點：穿過D內部且平行於x軸的直線，與D的邊界不多於兩點。

稱D為Y型區域，此時可採用先對x，后對y積分的積分次序，將二重定積分化為累次積分：

有許多二重積分僅僅依靠直角坐標下化為累次積分的方法難以達到簡化和求解的目的。當積分區域為圓域，環域，扇域等，或被積函數為 等形式時，採用極坐標會更方便。

在直角坐標系xOy中，取原點為極坐標的極點，取正x軸為極軸，則點P的直角坐標系（x，y）與極坐標軸（r，θ）之間有關係式：

在極坐標系下計算二重積分，需將被積函數f（x，y），積分區域D以及面積元素dσ都用極坐標表示。函數f（x，y）的極坐標形式為f（rcosθ，rsinθ）。為得到極坐標下的面積元素dσ的轉換，用坐標曲線網去分割D，即用以r=a，即O為圓心r為半徑的圓和以θ=b，O為起點的射線去無窮分割D，設Δσ就是r到r+dr和從θ到θ+dθ的小區域，其面積為，可得到二重積分在極坐標下的表達式：