多邊形數
多邊形數
多邊形數是可以排成正多邊形的整數。古代數學家發現某些數目的豆子或珠子可以排成正多邊形。例如10可以排成三角形如圖。
目錄
x
x x
x x x
x x x x
但它不能排成正方形，而9則可以：
x x x
x x x
x x x
有些數既可排成三角形，又可排成正方形，例如36（這些數稱為三角平方數）：
x x x x x x
x x x x x x
x x x x x x
x x x x x x
x x x x x x
x x x x x x
x
x x
x x x
x x x x
x x x x x
x x x x x x
x x x x x x x
x x x x x x x x
多邊形數可以幫助數數目。例如將一堆圓形的藥丸倒進一個等邊三角形的盒，便可以透過數每邊的藥丸數目來知道藥丸的數目。
將多邊形數擴充到下一個項的方法是，擴充某兩個相連的臂，然後將中間的空白處補上。下面的圖，每個增加的層用“+”表示。
三角形數
1:
+ x
3:
x x
+ + x x
6:
x x
x x x x
+ + + x x x
10:
x x
x x x x
x x x x x x
+ + + + x x x x
正方形數
1:
+ x
4:
x + x x
+ + x x
9:
x x + x x x
x x + x x x
+ + + x x x
16:
x x x + x x x x
x x x + x x x x
x x x + x x x x
+ + + + x x x x
五邊形數:
1:
+ x
5:
x x
+ + x x
+ + x x
12:
x x
x x x x
+ x x + x x x x
+ + x x
+ + + x x x
1是任何多邊形數的第一項。
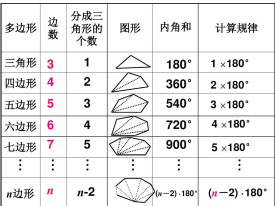
第n個s邊形數的公式是 \frac{n((s-2)n-(s-4))}{2}
費馬多邊形數定理指出每個數最多是n個n邊形的和。
基本信息
- 中文名
- 多邊形數
- 定義
- 可以排成正多邊形的整數
- 形式
- 一類整數
- 特點
- 可以排成正多邊形