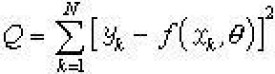非線性最小二乘法

式中 y是系統的輸出， x是輸入， θ是參數（它們可以是向量）。這裡的非線性是指對參數 θ的非線性模型，不包括輸入輸出變數隨時間的變化關係。在估計參數時模型的形式 f是已知的，經過 N次實驗取得數 據。估計參數的準則（或稱目標函數）選為模型的誤差平方和非線性最小二乘法就是求使 Q達到極小的參數估計值孌。

由於 f的非線性，所以不能像線性最小二乘法那樣用求多元函數極值的辦法來得到參數估計值，而需要採用複雜的優化演演算法來求解。常用的演演算法有兩類，一類是搜索演演算法，另一類是迭代演演算法。

搜索演演算法的思路是：按一定的規則選擇若干組參數值，分別計算它們的目標函數值並比較大小；選出使目標函數值最小的參數值，同時捨棄其他的參數值；然後按規則補充新的參數值，再與原來留下的參數值進行比較，選出使目標函數達到最小的參數值。如此繼續進行，直到選不出更好的參數值為止。以不同的規則選擇參數值，即可構成不同的搜索演演算法。常用的方法有單純形搜索法、複合形搜索法、隨機搜索法等。

迭代演演算法是從參數的某一初始猜測值 θ出發，然後產生一系列的參數點，如果這個參數序列收斂到使目標函數極小的參數點孌，那麼對充分大的 N就可用 N 作為孌。迭代演演算法的一般步驟是：

①　給出初始猜測值 θ，並置迭代步數 。

②　確定一個向量v作為第 i步的迭代方向。

③　用尋優的方法決定一個標量步長 ρ

④　檢查停機規則是否滿足，如果不滿足，則將 i加1再從②開始重複；如果滿足，則取 θ為值。

典型的迭代演演算法有牛頓－拉夫森法、高斯迭代演演算法、麥夸特演演算法、變尺度法等。

非線性最小二乘法除可直接用於估計靜態非線性模型的參數外，在時間序列建模、連續動態模型的參數估計中，也往往遇到求解非線性最小二乘問題。