模擬退火法
模擬退火法
模擬退火演演算法(Simulate Anneal Arithmetic,SAA)是一種通用概率演演演算法,用來在一個大的搜尋空間內找尋命題的最優解。模擬退火是S.Kirkpatrick, C.D.Gelatt和M.P.Vecchi在1983年所發明。而V.Černý在1985年也獨立發明此演演演算法。模擬退火演演算法是解決TSP問題的有效方法之一。
模擬退火來自冶金學的專有名詞退火。退火是將材料加熱后再經特定速率冷卻,目的是增大晶粒的體積,並且減少晶格中的缺陷。材料中的原子原來會停留在使內能有局部最小值的位置,加熱使能量變大,原子會離開原來位置,而隨機在其他位置中移動。退火冷卻時速度較慢,使得原子有較多可能可以找到內能比原先更低的位置。
模擬退火的原理也和金屬退火的原理近似:將熱力學的理論套用到統計學上,將搜尋空間內每一點想像成空氣內的分子;分子的能量,就是它本身的動能;而搜尋空間內的每一點,也像空氣分子一樣帶有“能量”,以表示該點對命題的合適程度。演演演算法先以搜尋空間內一個任意點作起始:每一步先選擇一個“鄰居”,然後再計算從現有位置到達“鄰居”的概率。
模擬退火演演算法可以分解為解空間、目標函數和初始解三部分。
模擬退火的基本思想:
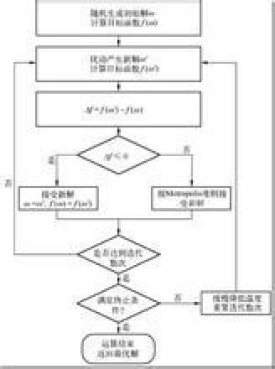
(1) 初始化:初始溫度T(充分大),初始解狀態S(是演演算法迭代的起點),每個T值的迭代次數L
(2) 對k=1,……,L做第(3)至第6步:
(3) 產生新解S′
(4) 計算增量Δt′=C(S′)-C(S),其中C(S)為評價函數
(5) 若Δt′<0則接受S′作為新的當前解,否則以概率exp(-Δt′/T)接手S′作為新的當前解.
(6) 如果滿足終止條件則輸出當前解作為最優解,結束程序。終止條件通常取為連續若干個新解都沒有被接受時終止演演算法。
(7) T逐漸減少,且T->0,然後轉第2步。
模擬退火演演算法新解的產生和接受可分為如下四個步驟:
第一步是由一個產生函數從當前解產生一個位於解空間的新解;為便於後續的計算和接受,減少演演算法耗時,通常選擇由當前新解經過簡單地變換即可產生新解的方法,如對構成前解的全部或部分元素進行置換、互換等,注意到產生新解的變換方法決定了當前新解的鄰域結構,因而對冷卻進度表的選取有一定的影響。
第二步是計算與新解所對應的目標函數差。因為目標函數差僅由變換部分產生,所以目標函數差的計算最好按增量計算。事實表明,對大多數應用而言,這是計算目標函數差的最快方法。
第三步是判斷新解是否被接受,判斷的依據是一個接受準則,最常用的接受準則是Metropolis準則: 若Δt′<0則接受S′作為新的當前解S,否則以概率exp(-Δt′/T)接受S′作為新的當前解S。
第四步是當新解被確定接受時,用新解代替當前解,這隻需將當前解中對應於產生新解時的變換部分予以實現,同時修正目標函數值即可。此時,當前解實現了一次迭代。可在此基礎上開始下一輪試驗。而當新解被判定為捨棄時,則在原當前解的基礎上繼續下一輪試驗。
模擬退火演演算法與初始值無關,演演算法求得的解與初始解狀態S(是演演算法迭代的起點)無關;模擬退火演演算法具有漸近收斂性,已在理論上被證明是一種以概率l 收斂於全局最優解的全局優化演演算法;模擬退火演演算法具有并行性。
作為模擬退火演演算法應用,討論旅行商問題(Travelling Salesman Problem,簡記為TSP):設有n個城市,用數碼(1,…,n)代表。城市i和城市j之間的距離為d(i,j) i, j=1,…,n.TSP問題是要找遍訪每個域市恰好一次的一條迴路,且其路徑總長度為最短。
求解TSP的模擬退火演演算法模型可描述如下:
解空間:解空間S是遍訪每個城市恰好一次的所有迴路,是{1,……,n}的所有循環排列的集合,S中的成員記為(w1,...,wn),並記wn + 1 = w1。初始解可選為(1,……,n)
目標函數:此時的目標函數即為訪問所有城市的路徑總長度或稱為代價函數:
我們要求此代價函數的最小值。
新解的產生 隨機產生1和n之間的兩相異數k和m,不妨設1<=kwm+1,…,wn)變為(w1,w2,…,wm,wk+1,…,wk,wm+1,…,wn)。
上述變換方法可簡單說成是“逆轉中間或者逆轉兩端”。
也可以採用其他的變換方法,有些變換有獨特的優越性,有時也將它們交替使用,得到一種更好方法。
代價函數差:設將(w1,w2,...,wn)變換為(u1,u2,...,un), 則代價函數差為:
根據上述分析,可寫出用模擬退火演演算法求解TSP問題的偽程序:
Procedure TSPSA:
begin
init-of-T; { T為初始溫度}
S={1,……,n}; {S為初始值}
termination=false;
while termination=false
begin
for i=1 to L do
begin
generate(S′form S); { 從當前迴路S產生新迴路S′}
Δt:=f(S′))-f(S);{f(S)為路徑總長}
IF(Δt<0) OR (EXP(-Δt/T)>Random-of-[0,1])
S=S′;
IF the-halt-condition-is-TRUE THEN
termination=true;
End;
T_lower;
End;
End
模擬退火演演算法的應用很廣泛,可以較高的效率求解最大截問題(Max Cut Problem)、0-1背包問題(Zero One Knapsack Problem)、圖著色問題(Graph Colouring Problem)、調度問題(Scheduling Problem)等等。
模擬退火演演算法的應用很廣泛,可以求解NP完全問題,但其參數難以控制,其主要問題有以下三點:
(1) 溫度T的初始值設置問題。
溫度T的初始值設置是影響模擬退火演演算法全局搜索性能的重要因素之一、初始溫度高,則搜索到全局最優解的可能性大,但因此要花費大量的計算時間;反之,則可節約計算時間,但全局搜索性能可能受到影響。實際應用過程中,初始溫度一般需要依據實驗結果進行若干次調整。
(2) 退火速度問題。
模擬退火演演算法的全局搜索性能也與退火速度密切相關。一般來說,同一溫度下的“充分”搜索(退火)是相當必要的,但這需要計算時間。實際應用中,要針對具體問題的性質和特徵設置合理的退火平衡條件。
(3) 溫度管理問題。
溫度管理問題也是模擬退火演演算法難以處理的問題之一。實際應用中,由於必須考慮計算複雜度的切實可行性等問題,常採用如下所示的降溫方式:
式中k為正的略小於1.00的常數,t為降溫的次數。