拿破崙定理
拿破崙·波拿巴提出的一個幾何定理
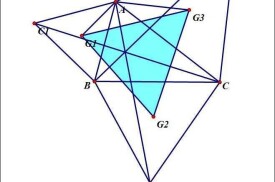
拿破崙定理則是法國著名的軍事家拿破崙·波拿巴已知最早提出的一個幾何定理:“徠以任意三角形的三條邊為邊,向外構造三個等邊三角形,則這三個等邊三角形的外接圓中心恰為另一個等邊三角形的頂點。”該等邊三角形稱為拿破崙三角形。如果向內(原三角形不需為等邊三角形)作三角形,結論同樣成立。
在△ABC的各邊上向外各作等邊△ABF,等邊△ACD,等邊△BCE。
如何證明:這3個等邊三角形的外接圓共點?
思路1:利用四點共圓來證明三圓共點。這是證明拿破崙定理的基礎。
證明:設等邊△ABF的外接圓和等邊△ACD的外接圓相交於O;連AO、CO、BO。
∴ ∠AFB=∠ADC=60°;
∵ A、F、B、O四點共圓;A、D、C、O四點共圓;
∴ ∠AOB=∠AOC=120°;
∴ ∠徠BOC=120°;
∵ △BCE是等邊三角形
∴ ∠BEC=60°;
∴ B、E、C、O四點共圓
∴ 這3個等邊三角形的外接圓共點。
拿破崙定理第三證明圖
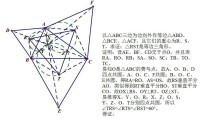
以任意三角形的三邊為邊向外作等邊三角形,則這三個等邊三角形的中心的連線是一個等邊三角形。
求證:上面3個等邊三角形的中心M、N、P的連線構成一個等邊三角形?
思路:利用已有的三個圓和三個四點共圓來證明。
證明:設等邊△ABD的外接圓⊙N,等邊△ACF的外接圓⊙M,等邊△BCE的外接圓⊙P
相交於O;連AO、CO、BO。
∵ A、D、B、O四點共圓;
A、F、C、O四點共圓
B、E、C、O四點共圓
∠AFC=∠ADB=∠BEC=60°;
∴ ∠AOB=∠AOC=∠BOC=120°;
∵ NP、MP、MN是連心線;
BO、CO、AO是公共弦;
∴ BO⊥NP於X;
CO⊥MP於Y;
AO⊥NM於Z。
∴ X、P、Y、O四點共圓;
Y、M、Z、O四點共圓;
Z、N、X、O四點共圓;
∴ ∠N=∠M=∠P=60°;
即△MNP是等邊三角形。
思路2:證明原三角形幾何中心至外圍三個等邊三角形幾何中心距離相等。
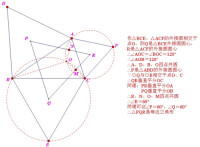
拿破崙定理
費馬點也是證明拿破崙定理的好方法。
右圖即是用費馬點的性質來推導拿破崙定理的證明方法。
思路3:用相似證明三邊相等
證明:如圖,分別以△ABC的邊BC、AC、AB為等邊三角形邊長,向△ABC外作等邊三角形(△BCC'、△ACA'、△ABB'),設這三個三角形的中心分別為D,E,F,
則:∠FAB=∠FBA=∠DBC=∠DCB=∠EAC=∠ECA=30°
以點A為圓心,以AF長為半徑作弧;以點E為圓心,以DC長為半徑作弧。設兩弧在多邊形AFBDCE內交於點G。則AG=AF,GE=DC。
連接GF、GA、GE,DE、DF、EF。
∵△ABF、△BCD、△ACE都是底角為30°的等腰三角形(即∠FAB=∠FBA=∠DBC=∠DCB=∠EAC=∠ECA=30°)
∴△ABF∽△BCD∽△ACE,
∴AF/AB = AE/AC = DC/BC 又∵AG=AF,GE=DC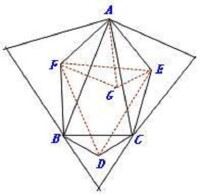

拿破崙定理
∴AG/AB = AE/AC = GE/BC
∴△AGE∽△ABC
∴∠GAE=∠BAC
∴∠FAG = ∠EAF-∠GAE = ∠EAF-∠BAC = ∠FAB+∠EAC = 60°
又∵AG=AF
∴△AGF為等邊三角形
∴AG=AF,∠AGF=60° ∵△AGE∽△ABC
∴∠AGE=∠ABC
又∵∠FBD = ∠ABC+∠FBA+∠DBC = ∠ABC+60°
∠FGE = ∠AGE+∠AGF = ∠AGE+60°
∴∠FBD=∠FGE
∵在△FBD和△FGE中,
FB=FG,∠FBD=∠FGE,BD=GE
∴△FBD≌△FGE(SAS)
∴FD=FE
同理,FD=DE
∵FD=DE=FE
∴△DEF為等邊三角形