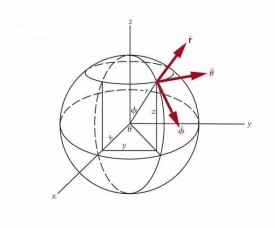
站心坐標系
以測站為原點的坐標系
站心坐標系也叫做站點坐標系、東-北-天坐標系ENU,英文名稱是local Cartesian coordinates coordinate system,主要是用於需了解以觀察者為中心的其他物體運動規律。
站心坐標系是以測站為原點的坐標系,即用準備好的基座來定點並進行觀察和測量,一般用於施工工程。也用於需了解以觀察者為中心的其他物體運動規律,如接收機可見GPS衛星的視角、方位角及距離等,需要用到站心坐標系。
站心直角坐標系
定義:以站心(如GPS接收天線中心)為坐標系原點O,Z軸與橢球法線重合,向上為正(天向),y與橢球短半軸重合(北向),x軸與地球橢球的長半軸重合(東向)所構成的直角坐標系,稱為當地東北天坐標系(ENU)。
站心極坐標系
定義:以站心為坐標極點O,以水平面(即xoy平面)為基準面,以東向軸(即x軸)為極軸,ρ為衛星到站點的距離,az為星視方向角(azimuth angle),el為星視仰角(elevation)。
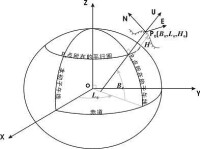
站心極坐標系
與空間直角坐標系之間的轉換
空間直角坐標變換為站心坐標的計算公式如下
站心坐標變換為空間直角坐標的計算公式如下
與大地坐標系之間的轉換
站心坐標系與大地坐標系之間也可以相互轉換。如果用戶從站心坐標系的原點運動到點,那麼這個位移量可先轉換成 ,然後再加上站心坐標系原點在地心地固坐標系的坐標得(x,y,z)最後根據《ECEF坐標系》中的公式得出大地坐標值及其變化量 。
反過來,大地坐標變化量也可藉助地心地固坐標系而轉換成站心坐標值 。可見站心坐標系與大地坐標系之間的變換需要不少的計算量,考慮到基準橢球體的偏心率e很小,因而為了減少計算量,又假設物體以低速運動,如果用戶在兩個測量時刻之間只運行上百米或上千米,那麼在絕大部分地區,的值與值比起來應該要小得多,在坐標變換過程中也就可以忽略之間的細微差別。近似運算公式為:
站心坐標系在使用過程中經常涉及坐標系的轉換,其中有些問題需要注意
1、坐標參照系包括基準和坐標系兩部分。
2、任一特定的基準和任一特定的坐標系的組合都形成特定地一個坐標參照系。
3、坐標系包括空間直角(X,Y,Z)、大地坐標系(B,L,H)、站心直角(N,E,U)和站心極坐標系(R,A,EL)等。
4、基準的作用就是給特定的坐標系進行特定的定位和定向。因此,一個坐標參照系必須同時包括基準和坐標系兩個部分才完整。
大地坐標系
以大地基準為基礎建立的坐標系稱為大地坐標系,也稱為橢球坐標系,用(B,L,H)來表示空間任一點的位置。其中,H是該點沿該點處法線至參考橢球面的距離即是我們通常所說的大地高。一般在工程測量當中我們很少使用大地高,而是使用正高或者正常高。
正高
是空間任一點沿該點處垂線至大地水準面的距離(與大地高的基準面不一樣)。
正常高
由於高程方向上的重力值很難精確表達出來,所以引入距離方向上的重力平均值來進行確定高程值,相應的基準面就是似大地水準面,因為它與大地水準面十分接近。
大地水準面差距
指的就是空間任一點大地高與正高的差值-------;
高程異常
指的就是空間任一點大地高與正常高的差值-------
空間直角坐標系
實質上點的空間直角坐標就是該點到坐標系原點形成的向徑在三個坐標軸上的投影;一般坐標系原點選在參考橢球的中心(參考橢球分為地心橢球和參心橢球),X軸指向本初子午線與赤道的交點,Z軸與地球自轉軸平行並指向參考橢球的北極,最終與Y軸形成右手直角坐標系。一般用(X,Y,Z)來表示任一點的空間位置。