抽象語言族

某些代數運算下具有封閉性的形式語言類，簡稱AFL。抽象語言族是用代數方法研究形式語言理論的重要成果。

基本定義 令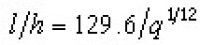∞為無限字母表，在其任一有限子集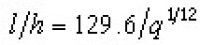i上構造語言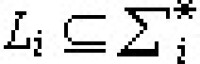。如果任何一組語言｛Li｝中至少包含一個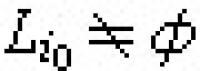，則稱｛Li｝為一語言族。

在同態、逆同態和與正則語言相交下保持封閉的語言族稱為滿三重組。對並運算封閉的滿三重組稱為滿半AFL。對乘冪閉包封閉的滿半 AFL稱為滿AFL。從一個語言族出發，經上述代數運算后得到的閉包分別稱為由生成的滿三重組、滿半AFL和滿AFL,以（）、()和（）表之。如果語言族只包含一個語言L，則由生成的結構分別稱為滿主三重組，滿主半AFL及滿主AFL。如果把同態限制為無空字同態，即不得把非空字映為空字，則所有以上定義中的“滿”字皆應除去。

判別準則 把非確定型有限自動機中的輸出字母推廣為輸出字母串，所得的裝置稱為a轉換器。把一個語言L的所有語句作輸入，全體輸出語句的集合即構成新語言L′。

一個語言族成為滿三重組的充分必要條件是它在 a轉換器運算下是封閉的。對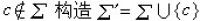。又對 K≥1構造任意的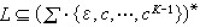。在上定義同態h為：h(c)＝ε,h(ɑ)＝ɑ(對任意ɑ∈)，則L中任一語句S不會比它的映像h(s)長K倍以上。因此稱h為K有界同態。所有的K有界同態統稱有界同態。

一個語言族成為 AFL的充分必要條件是它在並運算、無空字乘冪閉包、無空字正則置換、與正則語言相交及有界同態下是封閉的。

一個語言族成為滿 AFL的充分必要條件是它在並運算、乘冪閉包、正則置換、與正則語言相交及同態映射下是封閉的。

抽象接收器族 類似於從個別的語言到抽象語言族，從個別的自動機（接收器）出發也可得到相應的抽象接收器族，簡稱AFA。AFA接受語言族有兩種方式。如果只要求該AFA最後進入終止狀態，則接受的語言族正好是滿半AFL。如果除了要求AFA進入終止狀態外，還要求它的存儲同時變空，則接受的語言族正好是滿AFL。

喬姆斯基分層的四族語言0、1、2、3都是AFL,其中只有0、2、3是滿AFL。1不是，因為它在一般的同態映射下不封閉。