二面角

1.半平面：平面的一條直線把平面分成兩部分，其中每一部分都叫做一個半平面。

2.平面角：以二面角的公共直線上任意一點為端點，在兩個面內分別作垂直於公共直線的兩條射線，這兩條射線所成的角叫做二面角的平面角。二面角的大小可用平面角表示。

3.直二面角：平面角是直角的二面角叫做直二面角。互相垂直的平面：相交成直角的兩個平面叫做互相垂直的平面。

平面內的一條直線，把這個平面分為兩部分，每一部分都叫作半平面。從一條直線出發的兩個半平面所組成的圖形叫作二面角。這條直線叫作二面角的棱，這兩個半平面叫作二面角的面。二面角的大小，可以用它的平面角來度量，二面角的平面角是幾度，就說這個二面角是幾度。二面角也可以看作是從一條直線出發的一個半平面繞著這條直線旋轉，它的最初位置和最終位置組成的圖形。

二面角的平面角的大小，與其頂點在棱上的位置無關。如果兩個二面角能夠完全重合，則說它們是相等的．如果兩個二面角的平面角相等，那麼這兩個二面角相等。反之，相等二面角的平面角相等。

關於二面角的性質為：

(1)同一二面角的任意兩個平面角相等，較大二面角的平面角較大。

(2)兩個二面角的和或差所對應的平面角，是原來兩個二面角所對應的平面角的和或差。

(3)二面角可以平分，且平分面是唯一的。

(4)對棱二面角相等。

作二面角的平面角的常用方法有以下幾種：

1、定義法：在棱上取一點A，然後在兩個平面內分別作過棱上A點的垂線。有時也可以在兩個平面內分別作棱的垂線，再過其中的一個垂足作另一條垂線的平行線。

2、垂面法：作與棱垂直的平面，則垂面與二面角兩個面的交線所成的角就是二面角的平面角

3、面積射影定理：二面角的餘弦值等於某一個半平面在另一個半平面的射影的面積和該平面自己本身的面積的比值。即公式cosθ=（S'為射影面積，S為斜面面積）。運用這一方法的關鍵是從圖中找出斜面多邊形和它在有關平面上的射影，而且它們的面積容易求得。

4、三垂線定理及其逆定理法：先找到一個平面的垂線，再過垂足作棱的垂線，連接兩個垂足即得二面角的平面角。

5、向量法：分別作出兩個半平面的法向量，由向量夾角公式求得。二面角就是該夾角或其補角。

6、轉化法：在二面角α-l-β其中一個半平面α上找一點P，求出P到β的距離h和P到l的距離d，那麼arcsin()（二面角為銳角）或π-arcsin()（二面角為鈍角）就是二面角的大小。

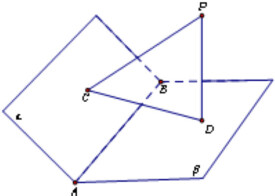
7、異面直線的距離法：設二面角為C-AB-D，其中AC和BD互為異面直線且AC⊥AB，BD⊥AB（即AB是異面直線AC和BD的公垂線）。設AB=d，CD=l，AC=m，BD=n，根據 來求異面直線所成角θ。利用該方法求θ必須先由圖像判斷二面角是銳角還是鈍角。如果是銳角，那麼取正號；鈍角，那麼取負號。待求出θ以後，如果二面角是銳角，那麼二面角的大小就是θ；鈍角，那麼二面角的大小就是π-θ。

其中，（1）、（2）點主要是根據定義來找二面角的平面角。

二面角一般都是在兩個平面的相交線上，取恰當的點，經常是端點和中點。過這個點分別在兩平面做相交線的垂線，然後把兩條垂線放到一個三角形中考慮。有時也經常做兩條垂線的平行線，使他們在一個更理想的三角形中。

（1）作出二面角的平面角

A：利用等腰(含等邊)三角形底邊的中點作平面角；

B：利用面的垂線（三垂線定理或其逆定理）作平面角；

C：利用與棱垂直的直線，通過作棱的垂面作平面角；

D：利用無棱二面角的兩條平行線作平面角。

（2）證明該角為平面角

（3）歸納到三角形求角

1）先建立直角坐標系，求出各點坐標；

2）設面的法向量為，面的法向量為；

3）然後求和 的夾角θ的餘弦

4）根據圖像觀察和的方向。如果兩個法向量一個指向二面角內部另一個指向二面角外部，則二面角的大小就是θ。如果兩個法向量同時指向二面角內部或外部，則二面角的大小為π-θ。