流體靜壓力
單位面積的流體靜壓強
設△S為ABCD平面上的任一面積,用△P表示作用在面積△S的總作用力,比值△P/△S的極限稱為流體靜壓強。因此,流體單位面積所受到垂直於該表面上的力稱為流體的靜壓強。習慣上,把流體靜壓強稱為靜壓力,或稱壓力,而將某一面積上所受到的靜壓力稱為總作用力。
在如下圖1所示的靜止溶液中,任取一點K,並在其周圍取微小面積△A,則相鄰流體對它就有作用力,設為△F。當微小面積趨於零時,K點的應力為:式中,p為靜止流體中的應力,稱為靜壓力,單位 或,有時也被稱為靜壓強。
流體靜壓力有兩個重要特性。
第一特性:流體靜壓力的方向沿作用面的內法線方向,或垂直指向作用面。
因為在靜止液體中,切應力等於零,又因為流體不能承受拉力而只能承受壓力.所以作用於流體上的唯一的表面力,只有指向作用面的內法線方向的靜壓力p。
第二特性:靜止流體中任意一點流體靜壓力的大小與作用面的方位無關,即任一點上各方向的流體靜壓力大小均相等。
流體平衡微分方程
在靜止流體中取邊長為的微元六面體,如下圖2所示,微小平行六面體各邊長度,各與相應的坐標軸平行。現在來分析這作用於微小六面體上的力。
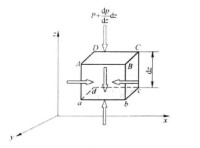
靜止流體中的微元六面體
由於壓力是坐標的連續函數,即,所以函數f按泰勒級數展開,並取該級數的前兩項,則可以得到與xy坐標面平行的六面體的另一面abcd上各點的壓力表示式,對於六面體的其他面上的壓力,也可以用上述方法寫出相應的表達式。
作用在微小平行六面體上的質量力為G,在一般情況下它可能是沿任一方向,它在x軸上的投影為,其中為流體的密度、為微小平行六面體的體積、X為單位質量力在x軸上的投影。
同樣,可以寫出質量力在x軸和在y軸上的投影。由於微小平行六面體處於靜止狀態,所以作用於其上的力在任一坐標軸的投影和等於零。對於X軸:
上式中,density為ρ,將上式中的各項除以ρdxdydz,即單位質量的作用力為 。對y軸和z軸採用同樣的方法處理,則得到:
以上計算式為流體平衡微分方程式,也稱歐拉平衡方程式。
重力場中的流體平衡方程
當流體處在重力場中面積質量僅有重力。單位質量流體所受質量力的3個分量應為(z軸以向上為正),將歐拉平衡方程式分別乘以並相加,得:
由於,則:
將單位質量流體所受質量力的三個分量帶入上式,得到:
對不可壓縮流體,ρ為常數,若對上式()按下圖3所示進行積分可得到:
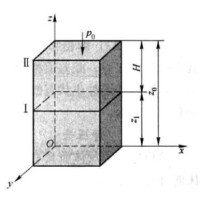
靜止流體的靜壓力
該式稱為不可壓縮流體靜力學基本方程。
