兩平面平行

兩平面間的位置關係

兩平面平行(parallelism between two planes)是兩平面間的一種位置關係，如果兩個平面沒有公共點，則稱這兩個平面有平行位置關係，簡稱兩平面相互平行，一個平面稱為另一個平面的平行平面。

目錄

1定義 2性質定理 3判定

定義

兩平面平行是兩平面間的一種位置關係，如果兩個平面沒有公共點，我們說這兩個平面互相平行，一個平面稱為另一個平面的平行平面。

性質定理

定理1　兩平面平行，其中一個平面內的直線必平行於另一個平面。

定理2　如果兩個平行平面同時和第三個平面相交，那麼它們的交線平行。

定理3　一條直線垂直於兩個平行平面中的一個平面，它也垂直於另一個平面。

例　如圖1，在正方體ABCD-ABCD中，M，N，P分別是CC，BC，CD的中點，求證：

(1)AP⊥MN；

(2)平面MNP∥平面ABD。

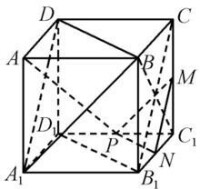
圖1

證明　(1)連結BC，BC，則BC⊥BC，BC是AP在面BBCC上的射影，

∴　AP⊥BC.

又BC∥MN，

∴　AP⊥MN.

(2)連結BD.

∵　P，N分別是DC，BC的中點，

∴　PN∥BD.又BD∥BD，

∴　PN∥BD.

又PN不在平面ABD上，

∴　PN∥平面ABD.

同理，MN∥平面ABD.

又PN∩MN=N，

∴　平面PMN∥平面ABD。

說明　將空間問題轉化為平面問題，是解決立體幾何問題的重要策略。解決這類問題關鍵在於選擇或添加適當的平面或線。由於M，N，P都為中點，故添加BC，BC作為聯繫的橋樑。

判定

判定定理

定理1

如果兩個平面垂直於同一條直線，那麼這兩個平面平行。

推論

如果兩個平面的垂線平行，那麼這兩個平面平行。

定理2

如果一個平面內有兩條相交直線與另一個平面平行，那麼這兩個平面平行。

定理3

如果一個平面內有兩條相交直線分別與另一個平面內的兩條相交直線平行，那麼這兩個平面平行。

目錄