切線長定理
初等平面幾何的一個定理
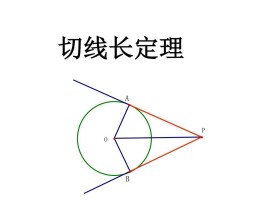
切線長定理(Theorem of length of tangent),是初等平面幾何的一個定理。它指出,從圓外一點引圓的兩條切線,它們的切線長相等。即如圖,AB、AC切圓O於B、C,切線長AB = AC。
切線長定理,是初等平面幾何的一個定理。在圓中,在經過圓外一點的切線,這一點和切點之間的線段叫做這點到圓的切線長。它指出,從圓外一點引圓的兩條切線,它們的切線長相等。
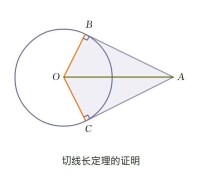
定理證明示意圖
欲證AC=AB,只需ABO ≌ ACO。
如圖,OC、OB為圓的兩條半徑,又∠ABO=∠ACO=90°
在RtABO和RtACO中
∴RtABO ≌ RtACO(H.L)
∴AB=AC,且∠AOB=∠AOC,且∠OAB=∠OAC。
切線長定理推論:
·圓的外切四邊形的兩組對邊的和相等;
·從圓外一點引圓的兩條切線,它們的切線長相等,圓心和這一點的連線平分兩條切線的夾角。
觀察、猜想、證明,形成定理
1、切線長的概念.如圖,P是⊙O外一點,PA,PB是⊙O的兩條切線,我們把線段PA,PB叫做點P到⊙O的 切線長.引導學生理解:切線和切線長是兩個不同的概念,切線是直線,不能度量;切線長是線段的長,這條線段的兩個端點分別是圓外一點和切點,可以度量。
2、觀察利用電腦變動點P的位置,觀察圖形的特徵和各量之間的關係.
3、猜想引導學生直觀判斷,猜想圖中PA是否等於PB.PA=PB.
4、證明猜想,形成定理.猜想是否正確。需要證明.組織學生分析證明方法.關鍵是作出輔助線OA,OB,要證明PA=PB.
想一想:根據圖形,你還可以得到什麼結論?∠OPA=∠OPB(如圖)等.
由此,引導學生推出切線長定理。
5、歸納:把前面所學的切線的5條性質與切線長定理一起歸納切線的性質
切線的性質:
(1)切線和圓只有一個公共點;
(2)切線和圓心的距離等於圓的半徑;
例題
(5)經過切點垂直於切線的直線必過圓心;
6、切線長定理的基本圖形研究
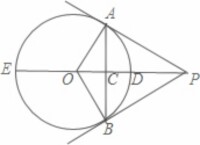
例如這道:如圖,PA,PB是⊙O的兩條切線,A,B為切點.直線OP交⊙O於點D,E,交AB於C
(1)寫出圖中所有的垂直關係;(2)寫出圖中所有的全等三角形;(3)寫出圖中所有的相似三角形;(4)寫出圖中所有的等腰三角形.
說明:對基本圖形的深刻研究和認識是在學習幾何中關鍵,它是靈活應用知識的基礎。
(鑽石形)
如右圖,AB、AC與⊙O相切,連接BC,設BC與AO交於點H。
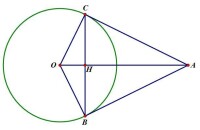
切線長定理
∵AB、AC與⊙O相切
∴∠ABO=∠ACO=90°
在Rt△ABO和Rt△ACO中
∠ABO=∠ACO=90°
BO=CO
AO=AO
∴RtΔABO≌RtΔACO(HL)
∴∠AOB=∠AOC
在△BOH和△COH
∠AOB=∠AOC
BO=CO
OH=OH
∴△BOH≌△COH(S.A.S)
∴∠BHO=∠CHO
∵∠BHO+∠CHO=180°
∴∠CHO=∠BHO=90°
∴BC⊥AO。
(或更簡單,∵RtΔABO≌RtΔACO(HL),易得RtΔABO與RtΔACO關於AO軸對稱。由軸對稱的性質:對稱軸垂直平分連接對應點的線段可得,BC⊥AO。)