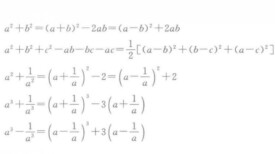恆等變形
恆等變形
恆等變形(identical deformation)是解析式的一種變換，把一個代數式變成另一個與它恆等的代數式，叫做恆等變形，或恆等變換。例如：由代數式4xy+3xy變成7xy是恆等變形。
將一個給定的解析式變換成另一個與它恆等的解析式，稱為解析式的恆等變形。恆等變形的具體意義有以下兩種：
1.若以為變數字母的解析式與g(x1，x2，…，xn)有相同的定義域D，且在D上等值，則f(x1，x2，…，xn)與在D上的相互替換，稱為恆等變形。例如在實數集R上，解析式可以互相替換。
恆等變形的更一般的意義是：若在所討論範圍內用表示同一關係的等號=聯繫著兩個式子，形成該討論範圍的一個恆等式，則稱這個恆等式兩端式子的相互替換為恆等變形。
【例1】證明：。
證明：設
則寫出的表達式
由於是實數，所以他們的和a也是實數，因為，由式（1）得即左端=。
【例2】證明：。
證明：設，則
所以但是
所以左端。
從例1和例2可以看到：兩個無理數的和或差可能是一個有理數或整數具體的例子。
基本信息
- 中文名
- 恆等變形
- 外文名
- identical deformation
- 所屬學科
- 數學
- 所屬問題
- 初等代數（解析式）
- 簡介
- 把代數式變成與它恆等的代數式
- 別名
- 恆等變換