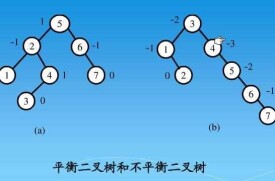
平衡樹

我們知道，對於一般的二叉搜索樹（Binary Search Tree），其期望高度（即為一棵平衡樹時）為logn，其各操作的時間複雜度（O(logn)）同時也由此而決定。但是，在某些極端的情況下（如在插入的序列是有序的時），二叉搜索樹將退化成近似鏈或鏈，此時，其操作的時間複雜度將退化成線性的，即O(n)。我們可以通過隨機化建立二叉搜索樹來盡量的避免這種情況，但是在進行了多次的操作之後，由於在刪除時，我們總是選擇將待刪除節點的後繼代替它本身，這樣就會造成總是右邊的節點數目減少，以至於樹向左偏沉。這同時也會造成樹的平衡性受到破壞，提高它的操作的時間複雜度。

平衡二叉搜索樹（Balanced Binary Tree）具有以下性質：它是一棵空樹或它的左右兩個子樹的高度差的絕對值不超過1，並且左右兩個子樹都是一棵平衡二叉樹。常用演演算法有紅黑樹、AVL、Treap、伸展樹等。在平衡二叉搜索樹中，我們可以看到，其高度一般都良好地維持在O（log（n）），大大降低了操作的時間複雜度。

紅黑樹是一種自平衡二叉查找樹，是在計算機科學中用到的一種數據結構，典型的用途是實現關聯數組。它是在1972年由Rudolf Bayer發明的，他稱之為"對稱二叉B樹"，它現代的名字是在 Leo J. Guibas 和 Robert Sedgewick 於1978年寫的一篇論文中獲得的。它是複雜的，但它的操作有著良好的最壞情況運行時間，並且在實踐中是高效的: 它可以在O(log n)時間內做查找，插入和刪除，這裡的n是樹中元素的數目。

AVL是最先發明的自平衡二叉查找樹演演算法。在AVL中任何節點的兩個兒子子樹的高度最大差別為一，所以它也被稱為高度平衡樹，n個結點的AVL樹最大深度約1.44log2n。查找、插入和刪除在平均和最壞情況下都是O（log n）。增加和刪除可能需要通過一次或多次樹旋轉來重新平衡這個樹。

Treap是一棵二叉排序樹，它的左子樹和右子樹分別是一個 Treap，和一般的二叉排序樹不同的是， Treap紀錄一個額外的數據，就是優先順序。 Treap在以關鍵碼構成二叉排序樹的同時，還滿足堆的性質(在這裡我們假設節點的優先順序大於該節點的孩子的優先順序)。但是這裡要注意的是 Treap和二叉堆有一點不同，就是二叉堆必須是完全二叉樹，而 Treap並不一定是。

伸展樹（Splay Tree）是一種二叉排序樹，它能在O(log n)內完成插入、查找和刪除操作。它由Daniel Sleator和Robert Tarjan創造。它的優勢在於不需要記錄用於平衡樹的冗餘信息。在 伸展樹上的一般操作都基於伸展操作。

Size Balanced Tree（簡稱 SBT）是一自平衡二叉查找樹，是在計算機科學中用到的一種數據結構。它是由中國廣東中山紀念中學的陳啟峰發明的。陳啟峰於2006年底完成論文《Size Balanced Tree》，並在2007年的全國青少年信息學奧林匹克競賽冬令營中發表。由於SBT的拼寫很容易找到中文諧音，它常被中國的信息學競賽選手和ACM/ICPC選手們戲稱為“傻B樹”、“Super BT”等。相比紅黑樹、AVL樹等自平衡二叉查找樹，SBT更易於實現。據陳啟峰在論文中稱，SBT是“目前為止速度最快的高級二叉搜索樹”。SBT能在O(log n)的時間內完成所有二叉搜索樹（BST）的相關操作，而與普通二叉搜索樹相比，SBT僅僅加入了簡潔的核心操作 Maintain。由於SBT賴以保持平衡的是size域而不是其他“無用”的域，它可以很方便地實現動態順序統計中的select和rank操作。