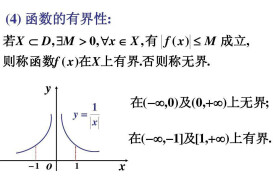
函數的有界性

設函數f(x)的定義域為D，f（x）集合D上有定義。

如果存在數K1，使得 對任意都成立，則稱函數f(x)在X上有上界。

反之，如果存在數字K使得 對任意都成立，則稱函數f(x)在D上有下界，而K稱為函數f(x)在D上的一個下界。

如果存在正數M，使得 對任意都成立，則稱函數在X上有界。如果這樣的M不存在，就稱函數f(x)在X上無界；等價於，無論對於任何正數M，總存在x1屬於X，使得|，那麼函數f(x)在X上無界。

此外，函數f(x)在X上有界的充分必要條件是它在X上既有上界也有下界。

一般來說，連續函數在閉區間具有有界性。例如: 在上有最小值7，最大值8，所以說它的函數值在7和8之間變化，是有界的，所以具有有界性。但正切函數在有意義區間，比如內則無界。

sinx，cosx，，， arcsinx，arccosx，arctanx，arccotx是常見的有界函數。

無窮小與有界函數的乘積仍為無窮小。