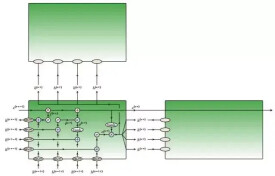
循環卷積
周期卷積的一種
循環卷積(circular convolution)不同於線性卷積的一種卷積運算,是周期卷積的一種。
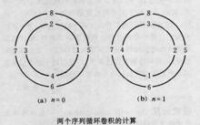
圖1
若求時刻的值,可將外圓的:固定,把內圓上的序列順時針旋轉一個單位時間(或將固定,把外圓上的序列逆時針旋轉),然後把對應項的乘積疊加起來,即為所求。如(b)圖所示,即
依圓序列循環移周,求:。所以循環卷積又稱圓周卷積,卷積結果y(n)長度仍等於N,其定義式
方括弧內的運算代表兩個周期序列的周期卷積。它與線性卷積不同之處是卷積過程只限在到的一個周期內。乘以表示卷積結果只取長度為N的主值序列。
由於離散傅里葉變換(DFT)的實質是周期序列變換到頻域的描述。可以證明:兩個有限長序列在時域的循環卷積,其DFT等於在頻域兩個序列相應的DFT的乘積。
式中和分別是和的N點DFT。它表明DFT具有循環卷積性質(CCP),也是區別於其他變換的重要特性。正是這種性質,用計算機通過計算DFT達到計算循環卷積和線性卷積的目的,提髙了運算效率。按長度為N的兩個序列,其線性卷積的長度應為,而循環卷積的長度仍然為N。為此,可以通過補零把序列長度增加到。這樣,一方面使循環卷積的長度等於線性卷積,另一方面避免進行循環卷積過程出現混疊造成失真,使計算結果與線性卷積相等,從而實現利用DFT計算線性卷積的目的。循環卷積有快速演演算法,廣泛應用於對通信系統的分析和綜合以及對信號的數字處理。
對於線性非時變離散時間系統來說,若序列x(n)是系統的輸入,h(n)是系統在單位脈衝作用下的單位脈衝響應,則由於輸入序列x(n)可表示為一系列脈衝的線性組合,所以,根據線性系統的疊加性質,系統的輸出在系統初始不儲能的條件下(零狀態響應)可由圖4式求得.
上式在運算過程存在序列的翻轉、移位、相乘和相加,所以稱為卷積和。表示兩個序列相卷積的運算符號,故式①也就是卷積的定義式。為了與離散傅里葉變換的循環卷積以及周期序列的周期卷積相區別,通常所指的卷積又稱為線性卷積。卷積運算符合交換率,可寫成另一種等效形式如圖5.
線性卷積的計算可以用解析法,也可以用圖解法。若兩個序列的長度分別為和,則卷積結果的總長度應為。
同理,對線性非時變連續系統來說,若連續時間信號x(t)是系統的輸入,h(t)是系統在單位脈衝作用下的單位衝激響應,則系統在零狀態的輸出為它們的卷積積分
線性卷積是數字信號處理中最常見的一種基本運算,不僅用於系統分析還用於系統設計。如果代表濾波器的脈衝響應則卷積運算就是一種線性濾波,y(n)是信號x(n)通過濾波器后的響應。
在實際問題中,碰到的問題大多數是求解線性卷積,例如,一個LSI系統,輸出y(n)為
下面將看到在一定條件下,可用循環卷積代替線性卷積,今後可看到循環卷積比線性卷積在計算速度上可提高許多倍。
設x(n)是長度為N的有限長序列,h(n)是長度為M的有限長度序列。
循環卷積是使用DFT(FFT)計算線性卷積時的衍生品。首先連續時間沒有循環卷積概念。離散時間時,不妨假設x(n)為L點信號,僅在有非零值;h(n)為M點信號,僅在有非零值。以x(n)為輸入信號通過以h(n)為單位衝激響應的線性時不變系統得到輸出,線性卷積,直接計算的複雜度為O(LM)。